Skip to article frontmatterSkip to article content

Métodos de volúmenes finitos para ecuaciones hiperbólicas

Ejemplos

Executable Books
Curvenote

https://rodin.uca.es/handle/10498/24890

%matplotlib widget
import sys
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FFMpegWriter, FuncAnimation
from tqdm.notebook import tqdm

1 Introducción

Los métodos de volúmenes finitos son técnicas del análisis numérico el cual surgen de la discretización de una EDP en su forma conservativa.

2 Fundamentos básicos

2.1 Ley de conservación

Una ley de conservación unidimensional es

Ut+fx(U)=0.U_{t}+ f_{x} \left(U\right) =0.
(1)

2.2 Sistemas lineales de leyes de conservación hiperbólicas

Ut+AUx=0.U_{t}+ AU_{x}= 0.
(2)

2.3 Problema de Cauchy

Si c∈Rc\in\mathbb{R} y f(U)=cUf\left(U\right)=cU, entonces U(x,t)=U0(x−ct)U\left(x,t\right)=U_{0}\left(x-ct\right).

2.4 Problema de Riemann

U0(x)={UL,x<x0,UR,x>x0.U_{0}\left(x\right)= \begin{cases} U_{\text{L}}, & x<x_{0},\\ U_{\text{R}}, & x>x_{0}. \end{cases}
(3)

donde UL,UR∈RU_{\text{L}}, U_{\text{R}}\in\mathbb{R}.

La solución es

U(x,t)={UL,x−ct<x0,UR,x−ct>x0.U\left(x,t\right)=\begin{cases} U_{\text{L}}, & x-ct<x_{0},\\ U_{\text{R}}, & x-ct>x_{0}.\\ \end{cases}
(4)

2.5 Velocidad de propagación en algunos problemas evolutivos

2.5.1 Problemas parabólicos

Ut−ΔU=0,x∈Ω⊂Rn,t>0.U_{t}-\Delta U=0, x\in\Omega\subset\mathbb{R}^{n}, t>0.
(5)

2.5.2 Problemas hiperbólicos

Utt−ΔU=0,x∈Ω⊂Rn,t>0.U_{tt}-\Delta U=0, x\in\Omega\subset\mathbb{R}^{n}, t>0.
(6)

3 Métodos de Volúmenes Finitos

Métodos descentrados de primer orden.

3.1 Método de Volúmenes Finitos

Uin+1=Uin−ΔtΔx(Fi+12n−Fi−12n).U^{n+1}_{i}= U^{n}_{i}- \frac{\Delta t}{\Delta x} \left( F^{n}_{i+\frac{1}{2}}- F^{n}_{i-\frac{1}{2}} \right).
(7)
Fi+12n≈1Δx∫tntn+1f(U(xi+12,t)) dt.F^{n}_{i+\frac{1}{2}}\approx \frac{1}{\Delta x} \int^{t^{n+1}}_{t_{n}} f \left( U \left(x_{i+\frac{1}{2}},t\right) \right) \,\mathrm{d}t.
(8)
Uin+1−UinΔt+Fi+12n−Fi−12nΔx=0.\frac{U^{n+1}_{i}-U^{n}_{i}}{\Delta t}+ \frac{F^{n}_{i+\frac{1}{2}}-F^{n}_{i-\frac{1}{2}}}{\Delta x}= 0.
(9)
Uin+1=Uin−ΔtΔx(ϕ(Uin,Ui+1n)−ϕ(Ui−1n,Uin)).U^{n+1}_{i}= U^{n}_{i}- \frac{\Delta t}{\Delta x} \left(\phi\left(U^{n}_{i},U^{n}_{i+1}\right)- \phi\left(U^{n}_{i-1},U^{n}_{i}\right)\right).
(10)

El método de volúmenes finitos es conservativo.

3.2 Métodos descentrados

3.2.1 Método descentrado upwind

Si c>0c>0,

Uin+1=Uin−cΔtΔx(Uin−Ui−1n).U^{n+1}_{i}= U^{n}_{i}- \frac{c\Delta t}{\Delta x} \left(U^{n}_{i}-U^{n}_{i-1}\right).
(11)

El flujo numérico a lo largo de la recta x=xi−12x=x_{i-\frac{1}{2}} es

Fi−12n=cUi−1n.F^{n}_{i-\frac{1}{2}}= cU^{n}_{i-1}.
(12)

El flujo numérico a lo largo de la recta x=xi+12x=x_{i+\frac{1}{2}} es

Fi+12n=cUin.F^{n}_{i+\frac{1}{2}}= cU^{n}_{i}.
(13)

3.2.1 Método descentrado downwind

Si c<0c<0,

Uin+1=Uin−cΔtΔx(Ui+1n−Uin).U^{n+1}_{i}= U^{n}_{i}- \frac{c\Delta t}{\Delta x} \left(U^{n}_{i+1}-U^{n}_{i}\right).
(14)

Fi+12n=cUi+1nF^{n}_{i+\frac{1}{2}}=cU^{n}_{i+1}, Fi−12n=cUinF^{n}_{i-\frac{1}{2}}=cU^{n}_{i}.

3.3 Método de Godunov

3.3.1 Primera versión

U~(x,tn)=Uin.\widetilde{U} \left(x,t_{n}\right)= U^{n}_{i}.
(15)
U~(xi−12,tn+1).\widetilde{U} \left( x_{i-\frac{1}{2}},t_{n+1} \right).
(16)
U~(xi+12,tn+1).\widetilde{U} \left( x_{i+\frac{1}{2}},t_{n+1} \right).
(17)
Uin+1=1Δx∫xi−12xiU~(xi−12,tn+1) dx+1Δx∫xixi+12U~(xi+12,tn+1) dx.U^{n+1}_{i}= \frac{1}{\Delta x} \int_{x_{i-\frac{1}{2}}}^{x_{i}} \widetilde{U} \left(x_{i-\frac{1}{2}},t_{n+1}\right)\, \mathrm{d}x+ \frac{1}{\Delta x} \int_{x_{i}}^{x_{i+\frac{1}{2}}} \widetilde{U}\left(x_{i+\frac{1}{2}},t_{n+1}\right)\, \mathrm{d}x.
(18)

3.3.2 Segunda versión

Fi+12n≈1Δt∫tntn+1f(U(xi+12,t)) dt.F^{n}_{i+\frac{1}{2}}\approx \frac{1}{\Delta t} \int_{t_{n}}^{t_{n+1}} f\left(U\left(x_{i+\frac{1}{2}},t\right)\right)\, \mathrm{d}t.
(19)

4 Convergencia, precisión y estabilidad

∥En∥=(Δx∑i=−∞+∞∣Ein∣2)12.\left\|E^{n}\right\|= {\left( \Delta x \sum_{i=-\infty}^{+\infty} {\left|E^{n}_{i}\right|}^{2} \right)}^{\frac{1}{2}}.
(20)
lim⁡Δt→0∥En∥2=0.\lim\limits_{\Delta t\to 0} {\left\|E^{n}\right\|}_{2}= 0.
(21)
∥En∥2=O(Δts), cuando Δt→0.{\left\|E^{n}\right\|}_{2}= \mathcal{O} \left(\Delta t^{s}\right), \text{ cuando } \Delta t\to 0.
(22)

Upwind

Uin+1=Uin−cΔtΔx(Uin−Ui−1n).U^{n+1}_{i}= U^{n}_{i}- c\frac{\Delta t}{\Delta x} \left(U^{n}_{i}-U^{n}_{i-1}\right).
(23)

Downwind

Uin+1=Uin−cΔtΔx(Ui+1n−Uin).U^{n+1}_{i}= U^{n}_{i}- c\frac{\Delta t}{\Delta x} \left(U^{n}_{i+1}-U^{n}_{i}\right).
(24)

FTCS

Uin+1=Uin−cΔt2Δx(Ui+1n−Ui−1n).U^{n+1}_{i}= U^{n}_{i}- c\frac{\Delta t}{2\Delta x} \left(U^{n}_{i+1}-U^{n}_{i-1}\right).
(25)

Lax-Friedrichs

Uin+1=12(Ui+1n+Ui−1n)−cΔt2Δx(Ui+1n−Ui−1n).U^{n+1}_{i}= \frac{1}{2} \left(U^{n}_{i+1}+U^{n}_{i-1}\right)- c\frac{\Delta t}{2\Delta x} \left(U^{n}_{i+1}-U^{n}_{i-1}\right).
(26)

Lax-Wendroff

Uin+1=Uin−cΔt2Δx(Ui+1n−Ui−1n)+c2Δt22Δx2(Ui+1n−2Uin+Ui−1n).U^{n+1}_{i}= U^{n}_{i}- c\frac{\Delta t}{2\Delta x} \left(U^{n}_{i+1}-U^{n}_{i-1}\right)+ c^{2} \frac{\Delta t^{2}}{2\Delta x^{2}} \left(U^{n}_{i+1}-2U^{n}_{i}+U^{n}_{i-1}\right).
(27)
Un+1=N(Un).U^{n+1}= \mathcal{N} \left(U^{n}\right).
(28)

4.2 Error de truncamiento local y consistencia

τn=1Δt(N(Un)−U^n+1).\tau^{n}= \frac{1}{\Delta t} \left( \mathcal{N} \left(U^{n}\right)- \hat{U}^{n+1} \right).
(29)
lim⁡Δt→0max⁡0≤n≤N−1∣τn∣=0.\lim_{\Delta t\to 0} \max_{0\leq n\leq N-1} \left|\tau^{n}\right|= 0.
(30)
τn=O(Δs).\tau^{n}= \mathcal{O}\left(\Delta^{s}\right).
(31)

4.3 Estabilidad

∥Un∥22≤K∥U0∥22.\left\|U^{n}\right\|^{2}_{2}\leq K \left\|U^{0}\right\|^{2}_{2}.
(32)

4.3.1 Condición CFL

∣cΔtΔx∣≤1.\left| c\frac{\Delta t}{\Delta x} \right|\leq 1.
(33)

4.3.2 Análisis de Estabilidad de Von Neumann

∣g(ξΔx)n∣≤1.\left| g\left(\xi\Delta x\right)^{n} \right|\leq 1.
(34)

5 Simulaciones numéricas

Introducimos las condiciones de contorno.

5.1 Condiciones de contorno

Extender el dominio computacional para incluir celdas en cada extremo, estas se llaman las celdas fantasmas.

Las condiciones de contorno periódicas,

  • Si c>0c>0, U0n=UNnU^{n}_{0}=U^{n}_{N}.

  • Si c<0c<0, UN+1n=U1nU^{n}_{N+1}=U^{n}_{1}.

∂U∂n=0, para x∈∂Ω.\frac{\partial U}{\partial n}=0, \text{ para }x\in\partial\Omega.
(35)

5.2 Lenguaje de programación Julia

               _
   _       _ _(_)_     |  Documentation: https://docs.julialang.org
  (_)     | (_) (_)    |
   _ _   _| |_  __ _   |  Type "?" for help, "]?" for Pkg help.
  | | | | | | |/ _` |  |
  | | |_| | | | (_| |  |  Version 1.11.2 (2024-12-01)
 _/ |\__'_|_|_|\__'_|  |  
|__/                   |

julia>

5.3 Test numéricos

5.3.1 Primeros test

Ut+cUx=0,x∈R,t>0U_{t}+cU_{x}=0,\quad x\in\mathbb{R},\quad t>0
(36)

Ejemplo 1

Ω=[0,20]\Omega=\left[0,20\right], Δx=0.1\Delta x=0.1, Δt=0.02\Delta t=0.02, c=−1c=-1.

U0(x)=e−(x−15)2.U_{0}\left(x\right)= e^{-{\left(x-15\right)}^{2}}.
(37)
plt.style.use("seaborn-v0_8-white")
def U(x):
    return np.exp(-np.power(x - 15, 2))
x = np.linspace(start=0, stop=20, num=300)
t, Δt = np.linspace(start=0, stop=1, num=51, retstep=True)
c = -1
fig, ax = plt.subplots(layout="constrained")
ax.plot(
    x,
    U(x),
    color="red",
    label=r"$U_{0}\left(x\right)$",
    linestyle="solid",
    linewidth=1.0,
)
ax.spines["bottom"].set_color("none")
ax.spines["top"].set_alpha(alpha=0.8)
ax.spines["top"].set_edgecolor(color="gray")
ax.spines["top"].set_linewidth(w=0.5)
ax.spines["left"].set_alpha(alpha=0.8)
ax.spines["left"].set_edgecolor(color="gray")
ax.spines["left"].set_linewidth(w=0.5)
ax.spines["right"].set_alpha(alpha=0.8)
ax.spines["right"].set_edgecolor(color="gray")
ax.spines["right"].set_linewidth(w=0.5)
ax.set_xlim(left=x[0], right=x[-1])
ax.set_ylim(bottom=0, top=1)
ax.set_title(
    label=r"Condición inicial $U_{0}\left(x\right)=e^{-{\left(x-15\right)}^{2}}$",
    loc="center",
)
ax.legend(loc="best")
Loading...

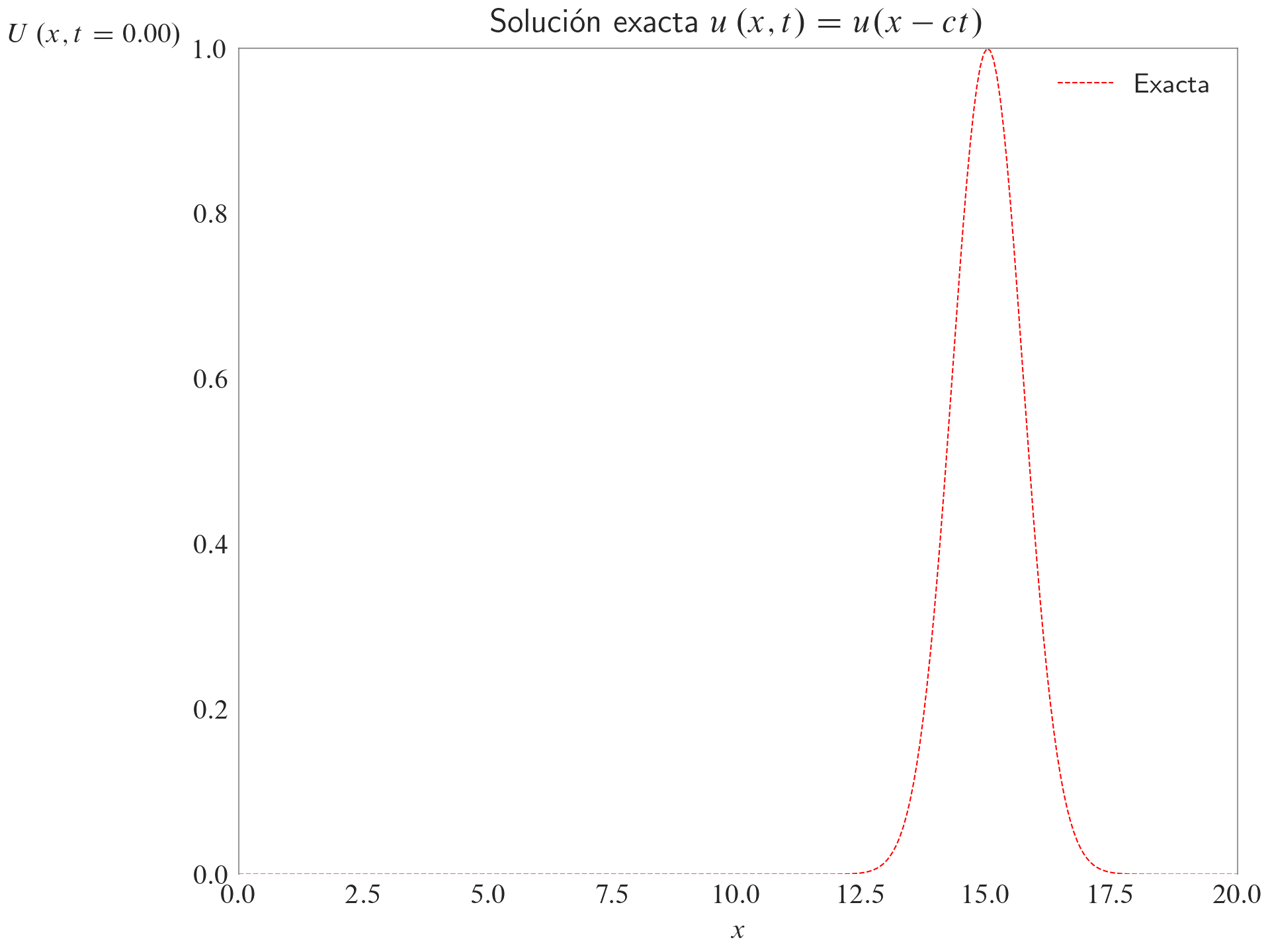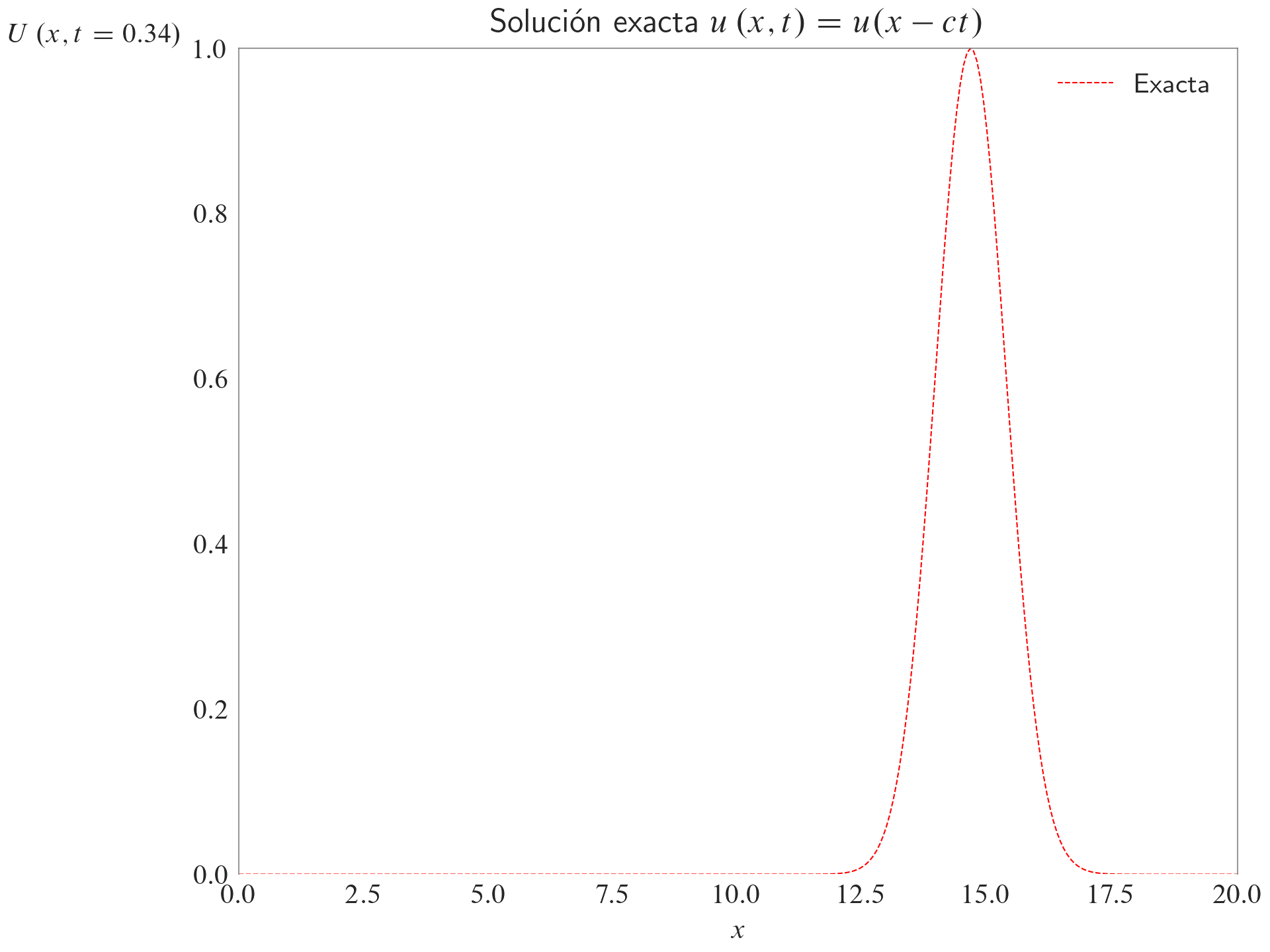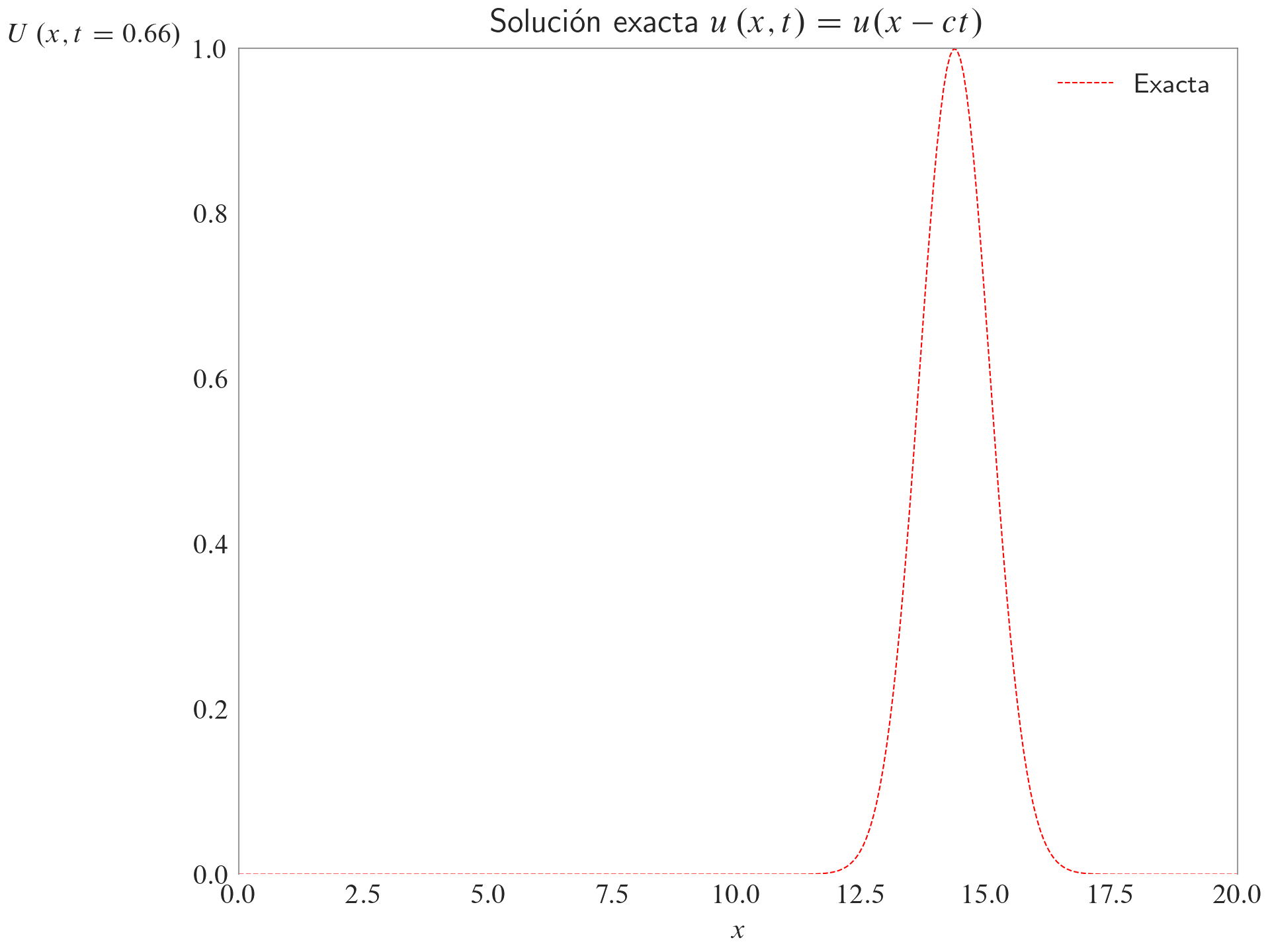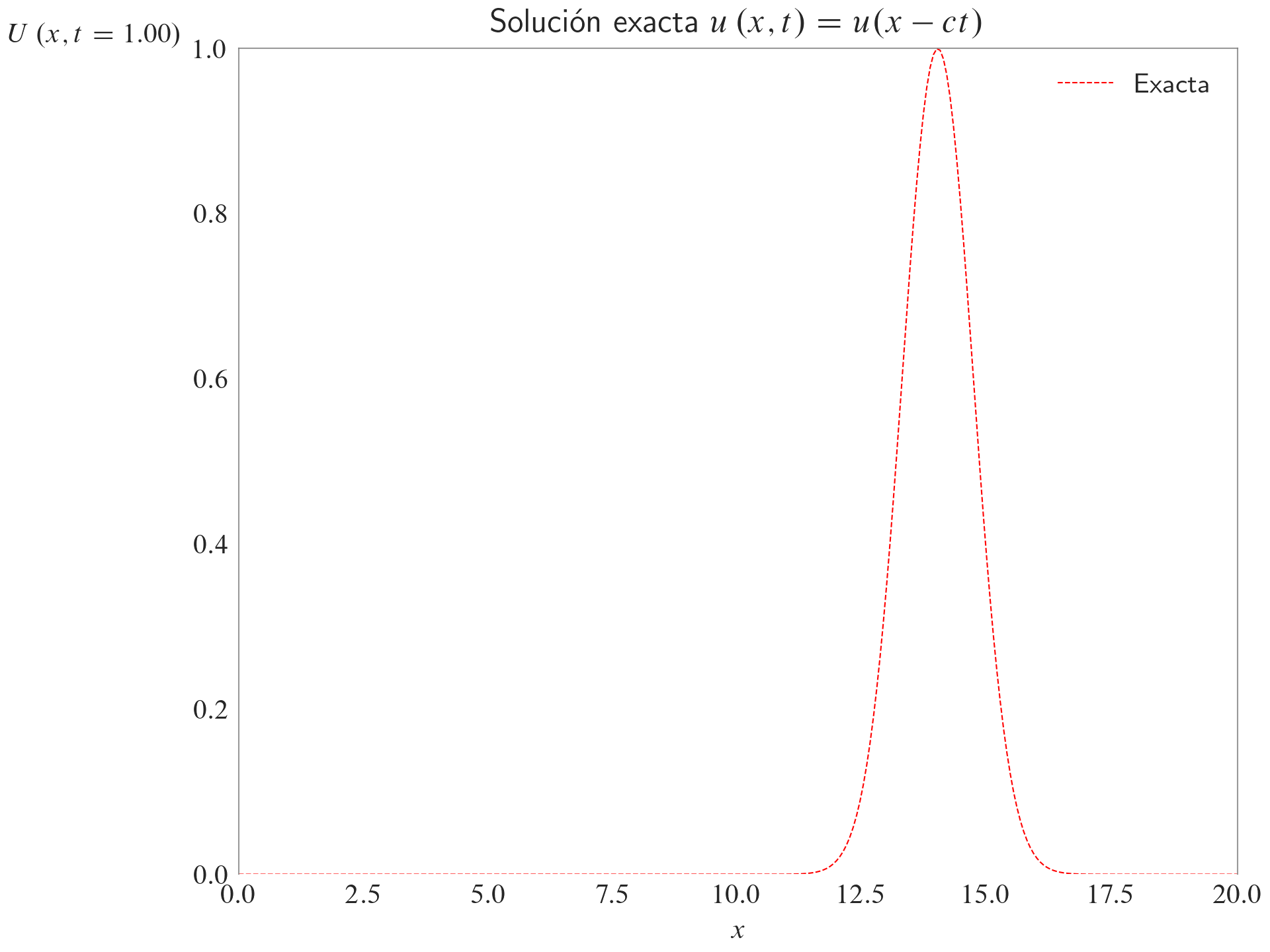
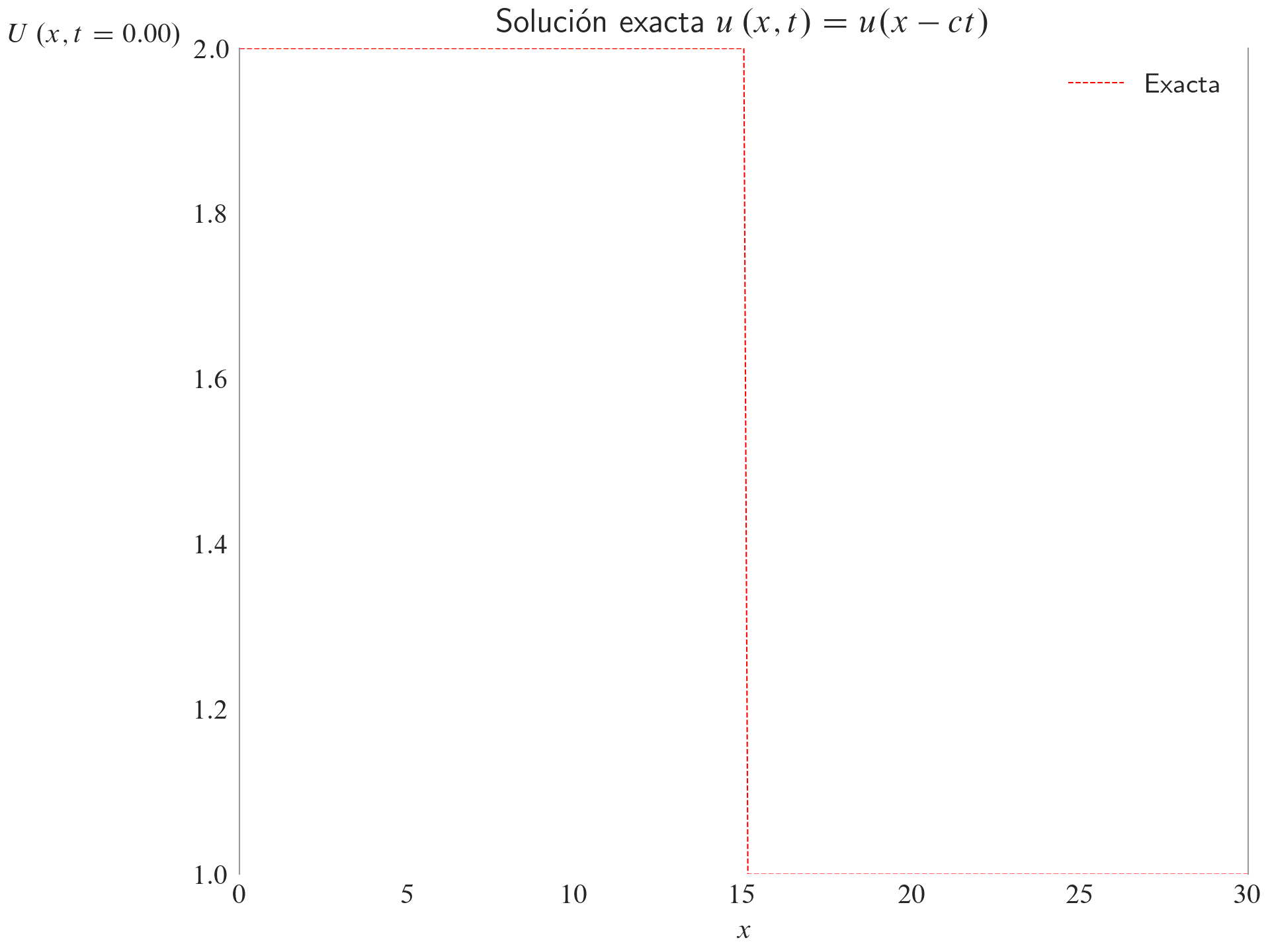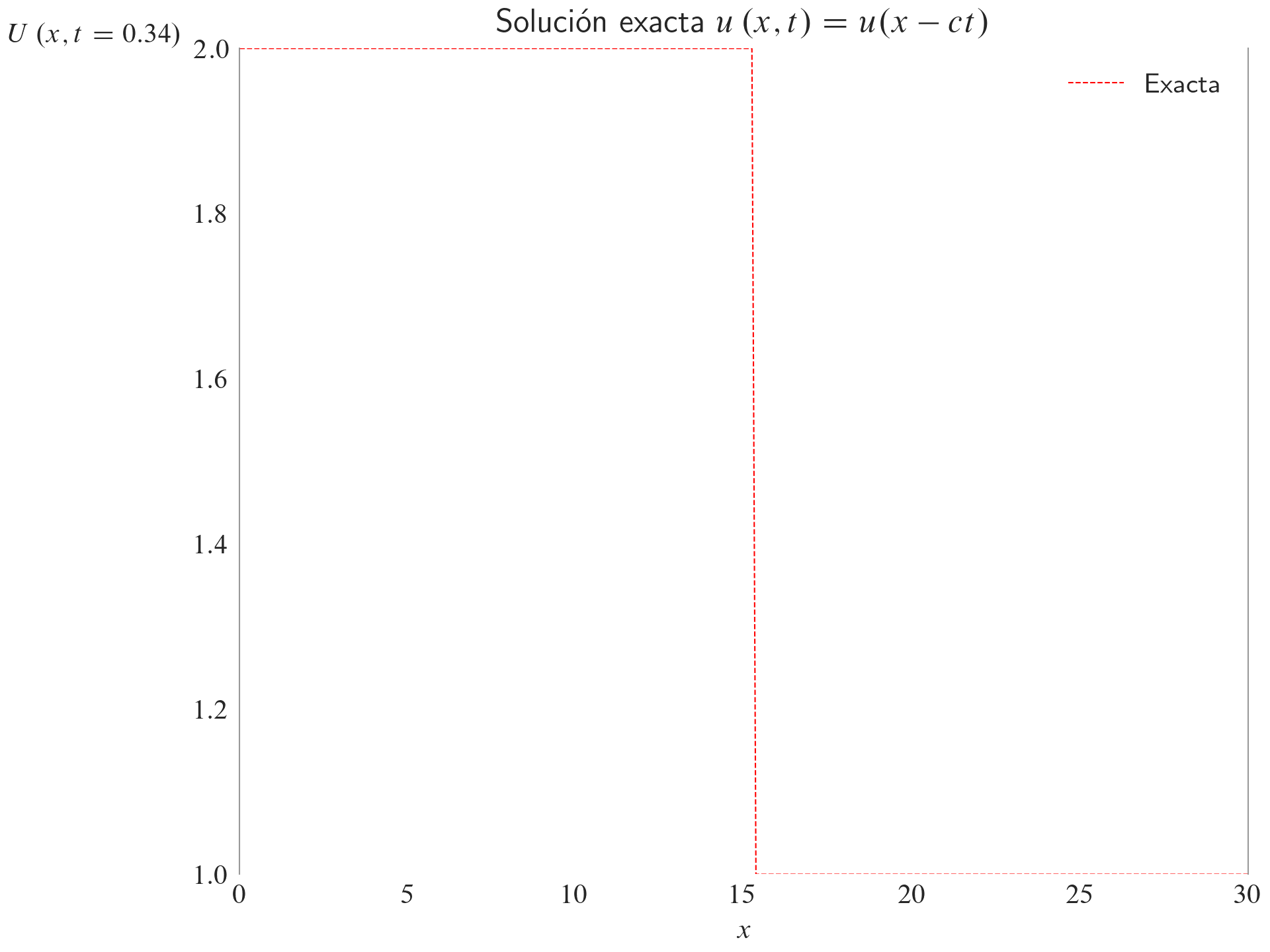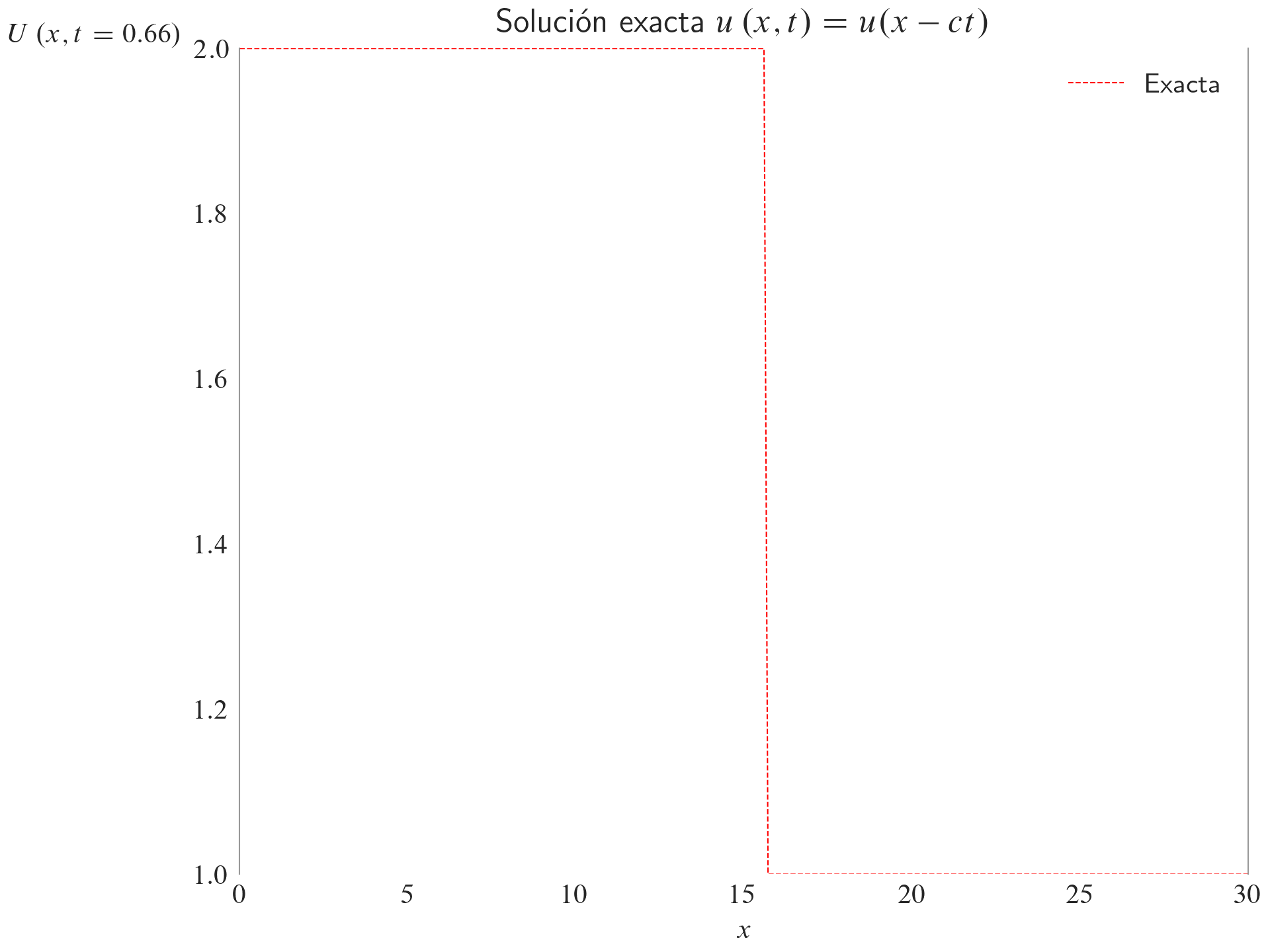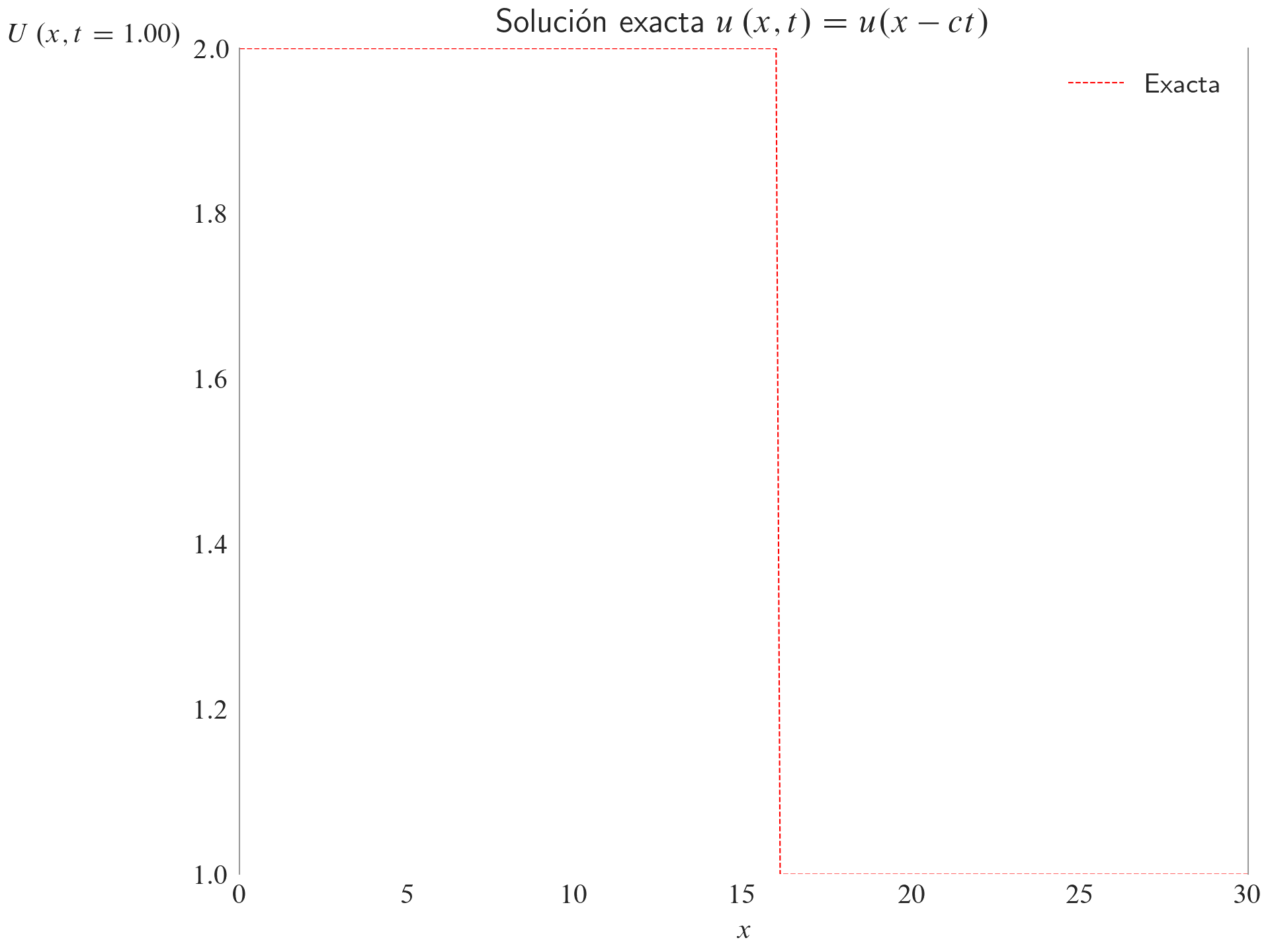
Solución exacta

fig, ax = plt.subplots(layout="constrained")
(ln,) = ax.plot(
    [],
    [],
    color="red",
    label="Exacta",
    linestyle="dashed",
    linewidth=0.5,
)
ax.spines["bottom"].set_color("none")
ax.spines["top"].set_alpha(alpha=0.8)
ax.spines["top"].set_edgecolor(color="gray")
ax.spines["top"].set_linewidth(w=0.5)
ax.spines["left"].set_alpha(alpha=0.8)
ax.spines["left"].set_edgecolor(color="gray")
ax.spines["left"].set_linewidth(w=0.5)
ax.spines["right"].set_alpha(alpha=0.8)
ax.spines["right"].set_edgecolor(color="gray")
ax.spines["right"].set_linewidth(w=0.5)
ax.set_xlabel(xlabel=r"$x$")
ax.set_xlim(left=x[0], right=x[-1])
ax.set_ylim(bottom=0, top=1)
ax.set_title(label=r"Solución exacta $u\left(x,t\right)=u(x-ct)$")
ax.legend(loc="best")

def init():
    ln.set_data(x, U(x))

    return (ln,)


def update(frame):
    ln.set_data(x, U(x=x - c * (t[0] + frame * Δt)))
    ax.set_ylabel(
        ylabel=rf"$U\left(x, t={frame * Δt:.2f}\right)$", loc="top", rotation=0
    )

    return (ln,)


anim = FuncAnimation(
    fig=fig,
    func=update,
    frames=tqdm(iterable=range(t.size), file=sys.stdout, colour="green"),
    interval=1,
    init_func=init,
    blit=True,
).save(
    filename="exactgaussian.gif",
    writer=FFMpegWriter(
        fps=90,
        codec="libx265",
        metadata={
            "subject": "Numerical Analysis",
            "title": "Exact solution Gaussian Function",
            "author": "Gloria Almozara Sainz",
            "genre": "Mathematics",
            "copyright": "2025",
            "srcform": "Matplotlib 3.9.3",
            "comment": "Numerical Simulation for advection PDE",
        },
    ),
    dpi=300,
    savefig_kwargs={"transparent": True, "facecolor": "none"},
)
plt.close()
Loading...

Método Downwind

Uin+1=Uin−cΔtΔx(Ui+1n−Uin).U^{n+1}_{i}= U^{n}_{i}- c\frac{\Delta t}{\Delta x} \left(U^{n}_{i+1}-U^{n}_{i}\right).
(38)
x, Δx = np.linspace(start=0, stop=20, num=201, retstep=True)
c = -1
cfl = c * Δt / Δx
fig, ax = plt.subplots(layout="constrained")

(ln,) = ax.plot(
    [],
    [],
    color="DarkBlue",
    label="Exacta",
    linestyle="dashed",
    linewidth=0.5,
)
ln1 = ax.scatter(
    x=[],
    y=[],
    c="blue",
    label=rf"CFL $={cfl:.1f}$, $\Delta x={Δx:.3f}$",
    s=0.4,
)
ax.set_xlabel(xlabel=r"$x$")
ax.set_xlim(left=x[0], right=x[-1])
ax.set_ylim(bottom=0, top=1)
ax.spines["bottom"].set_color("none")
ax.spines["top"].set_alpha(alpha=0.8)
ax.spines["top"].set_edgecolor(color="gray")
ax.spines["top"].set_linewidth(w=0.5)
ax.spines["left"].set_alpha(alpha=0.8)
ax.spines["left"].set_edgecolor(color="gray")
ax.spines["left"].set_linewidth(w=0.5)
ax.spines["right"].set_alpha(alpha=0.8)
ax.spines["right"].set_edgecolor(color="gray")
ax.spines["right"].set_linewidth(w=0.5)
ax.set_title(label="Método Downwind para la función gaussiana", loc="center")
ax.legend(loc="best")

U1 = U(x=x)


def init():
    ln.set_data(x, U(x))
    ln1.set_offsets(offsets=np.column_stack([x, U1]))

    return (ln,)


def update(frame):
    ln1.set_offsets(offsets=np.column_stack([x, U1]))
    ln.set_data(x, U(x=x - c * frame * Δt))
    U1[1:] -= cfl * (np.roll(U1, -1) - U1)[1:]
    ax.set_ylabel(
        ylabel=rf"$U\left(x, t={frame * Δt:.2f}\right)$", loc="top", rotation=0
    )

    return (ln,)


anim = FuncAnimation(
    fig=fig,
    func=update,
    frames=tqdm(iterable=range(t.size), file=sys.stdout, colour="green"),
    interval=1,
    init_func=init,
    blit=True,
).save(
    filename="downwindgaussian.gif",
    writer=FFMpegWriter(
        fps=90,
        codec="libx265",
        metadata={
            "subject": "Numerical Analysis",
            "title": "Exact solution",
            "author": "Gloria Almozara Sainz",
            "genre": "Mathematics",
            "copyright": "2025",
            "srcform": "Matplotlib 3.9.3",
            "comment": "Numerical Simulation for advection PDE",
        },
    ),
    dpi=300,
    savefig_kwargs={"transparent": True, "facecolor": "none"},
)
plt.close()
Loading...

Método Lax-Friedrichs

Uin+1=12(Ui+1n+Ui−1n)−cΔt2Δx(Ui+1n−Ui−1n).U^{n+1}_{i}= \frac{1}{2} \left(U^{n}_{i+1}+U^{n}_{i-1}\right)- c\frac{\Delta t}{2\Delta x} \left(U^{n}_{i+1}-U^{n}_{i-1}\right).
(39)
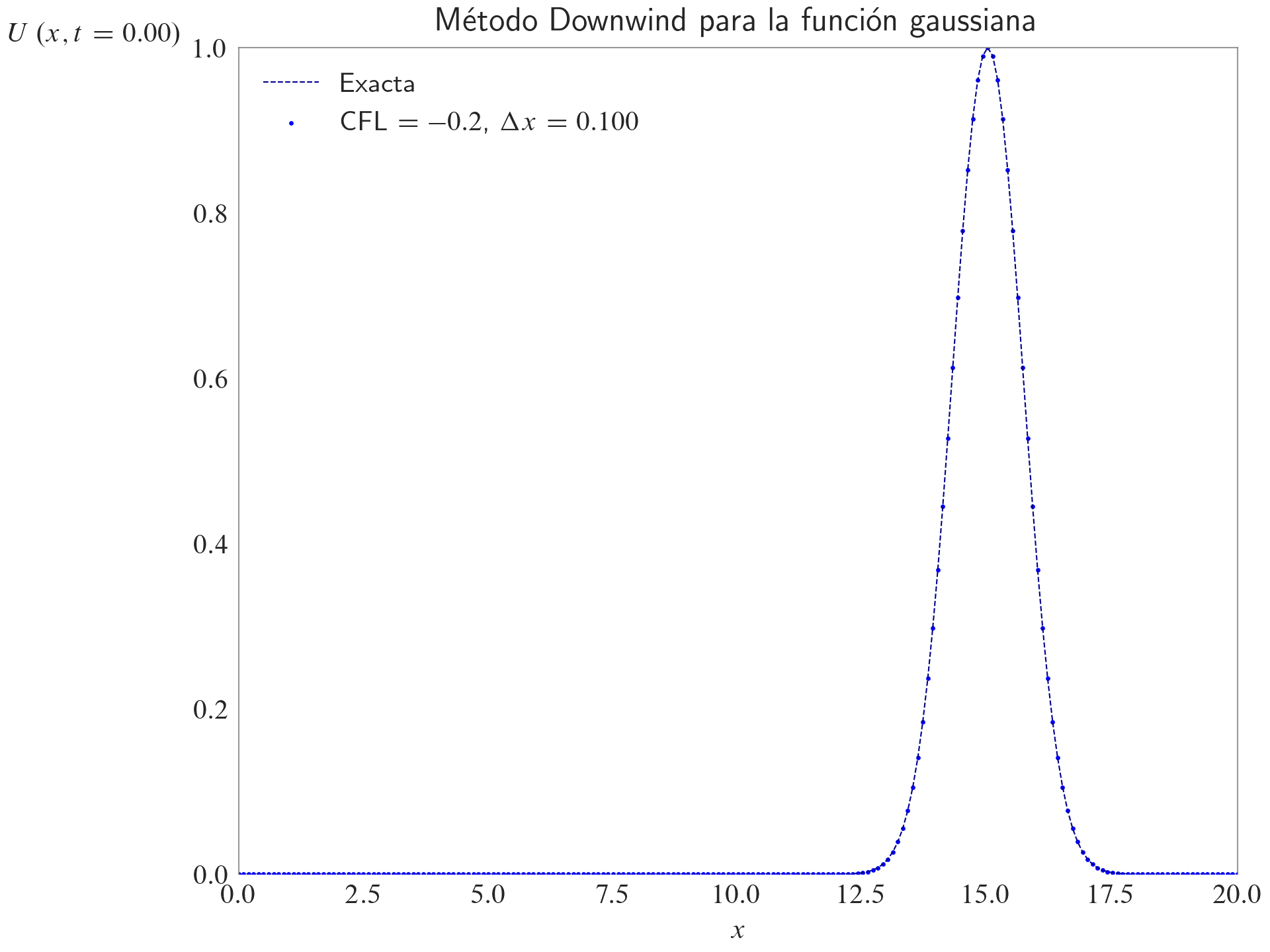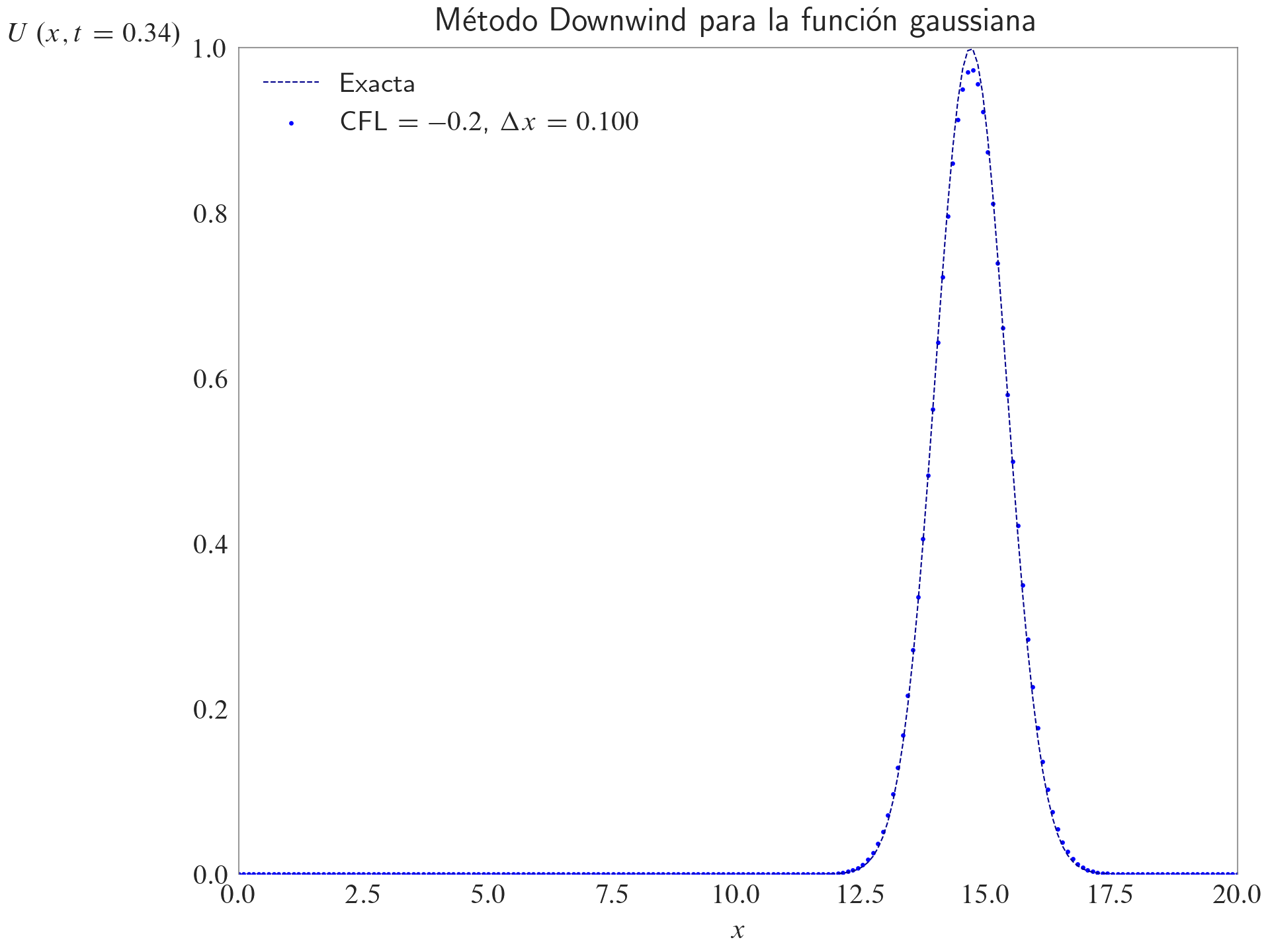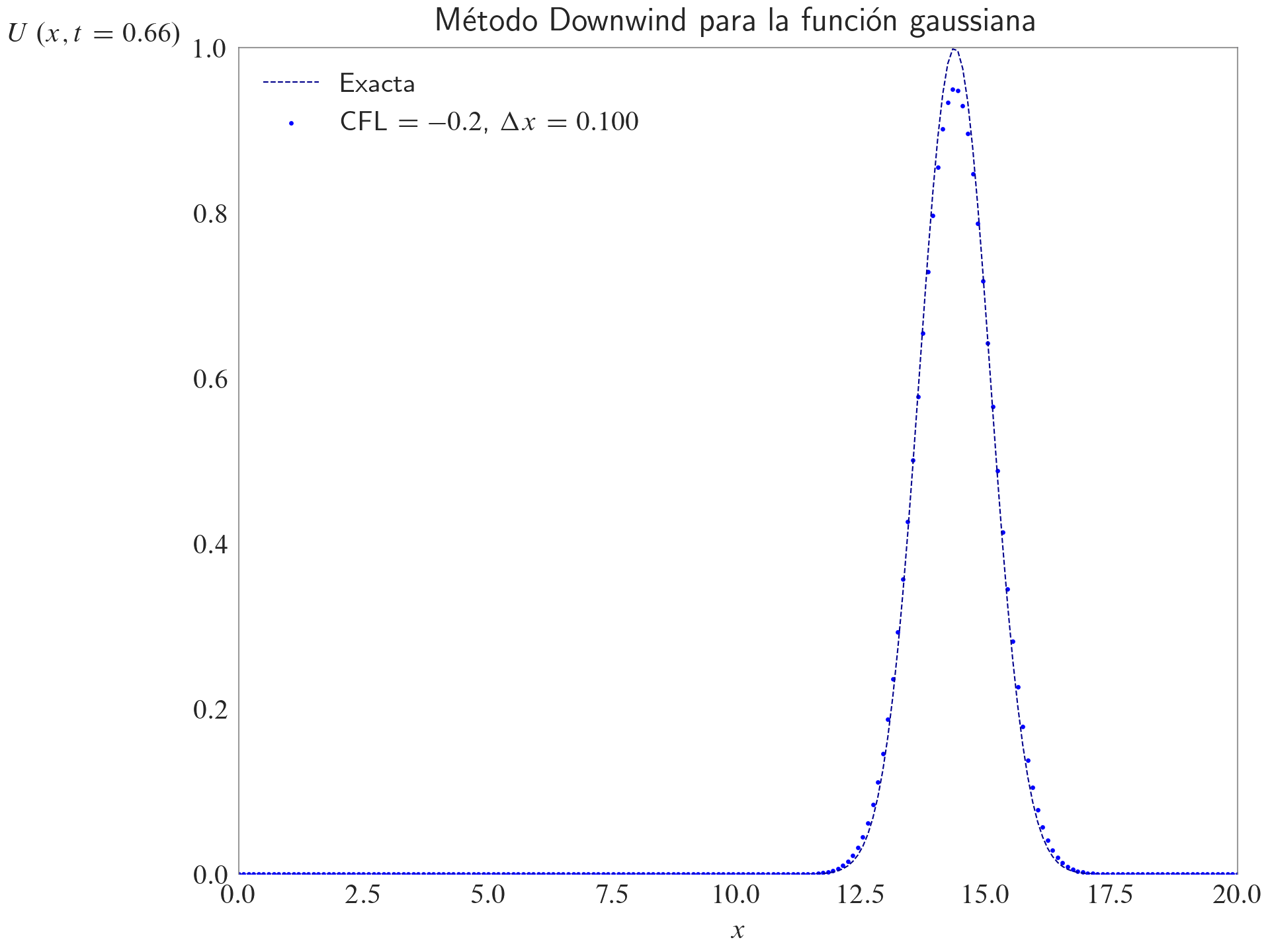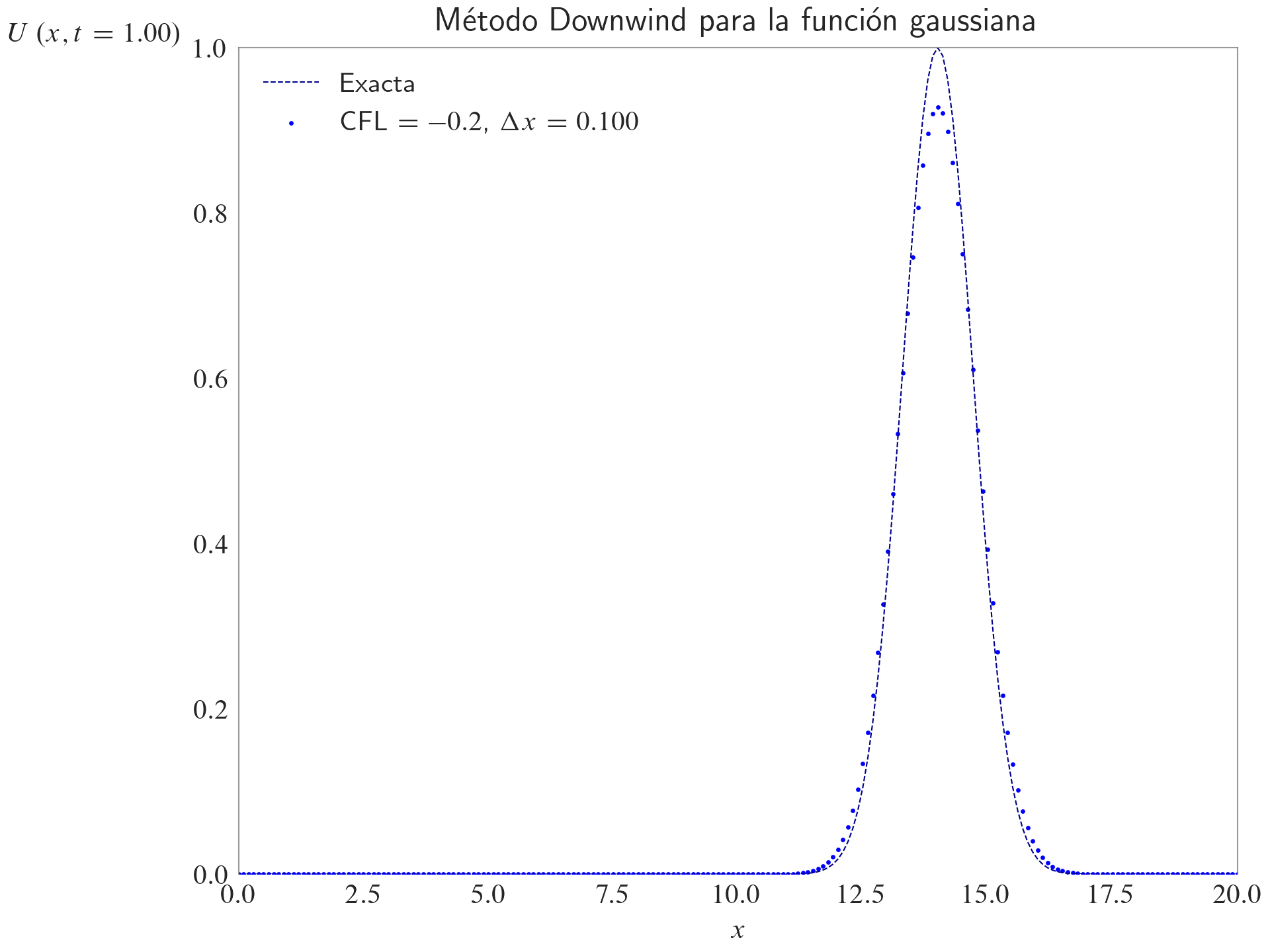
fig, ax = plt.subplots(layout="constrained")

(ln,) = ax.plot(
    [],
    [],
    color="DarkBlue",
    label="Exacta",
    linestyle="dashed",
    linewidth=0.5,
)

ln1 = ax.scatter(
    x=[],
    y=[],
    c="blue",
    label=rf"CFL $={cfl:.1f}$, $\Delta x={Δx:.3f}$",
    s=0.4,
)
ax.set_xlabel(xlabel=r"$x$")
ax.set_xlim(left=x[0], right=x[-1])
ax.set_ylim(bottom=0, top=1)
ax.spines["bottom"].set_color("none")
ax.spines["top"].set_alpha(alpha=0.8)
ax.spines["top"].set_edgecolor(color="gray")
ax.spines["top"].set_linewidth(w=0.5)
ax.spines["left"].set_alpha(alpha=0.8)
ax.spines["left"].set_edgecolor(color="gray")
ax.spines["left"].set_linewidth(w=0.5)
ax.spines["right"].set_alpha(alpha=0.8)
ax.spines["right"].set_edgecolor(color="gray")
ax.spines["right"].set_linewidth(w=0.5)
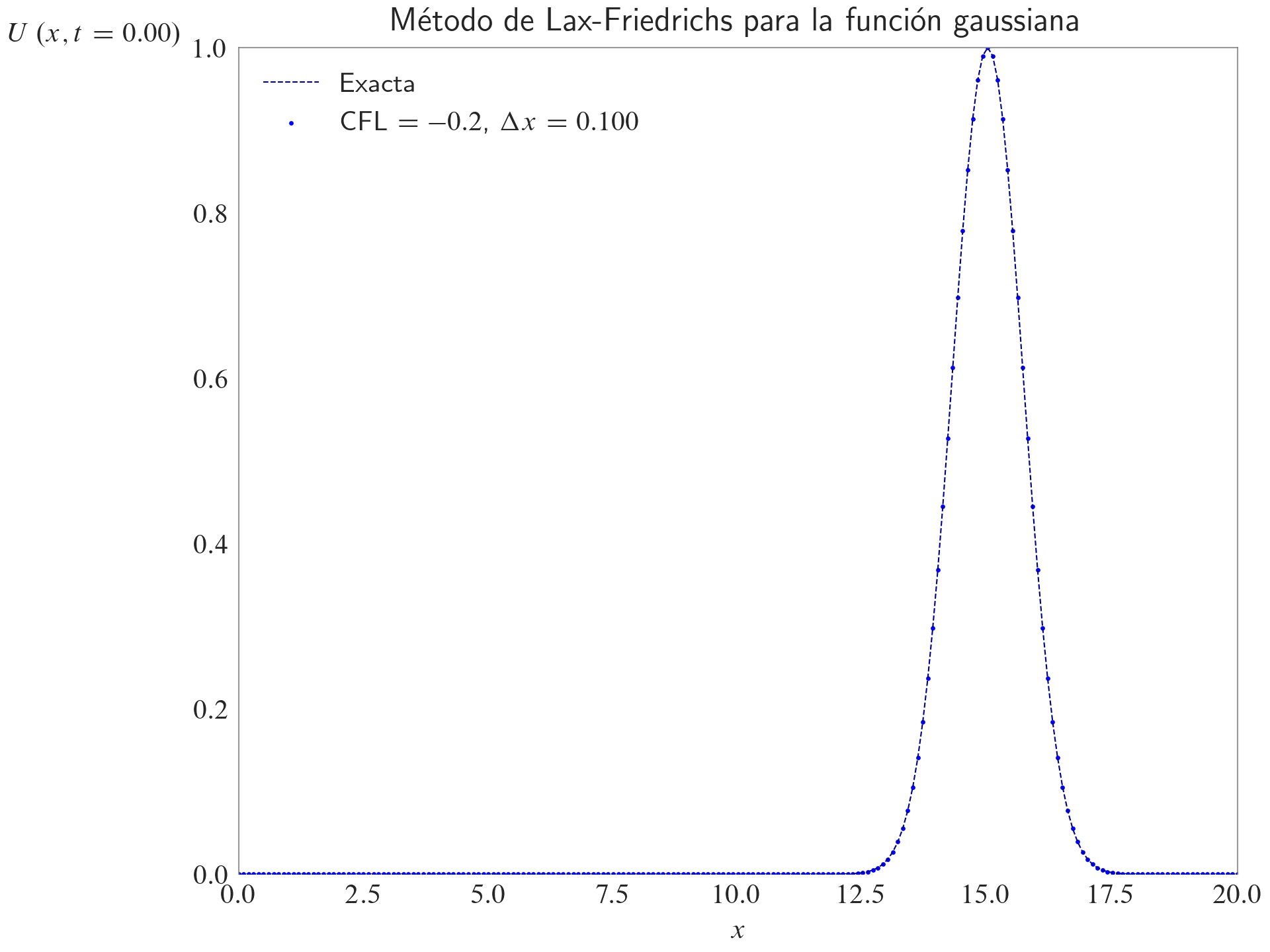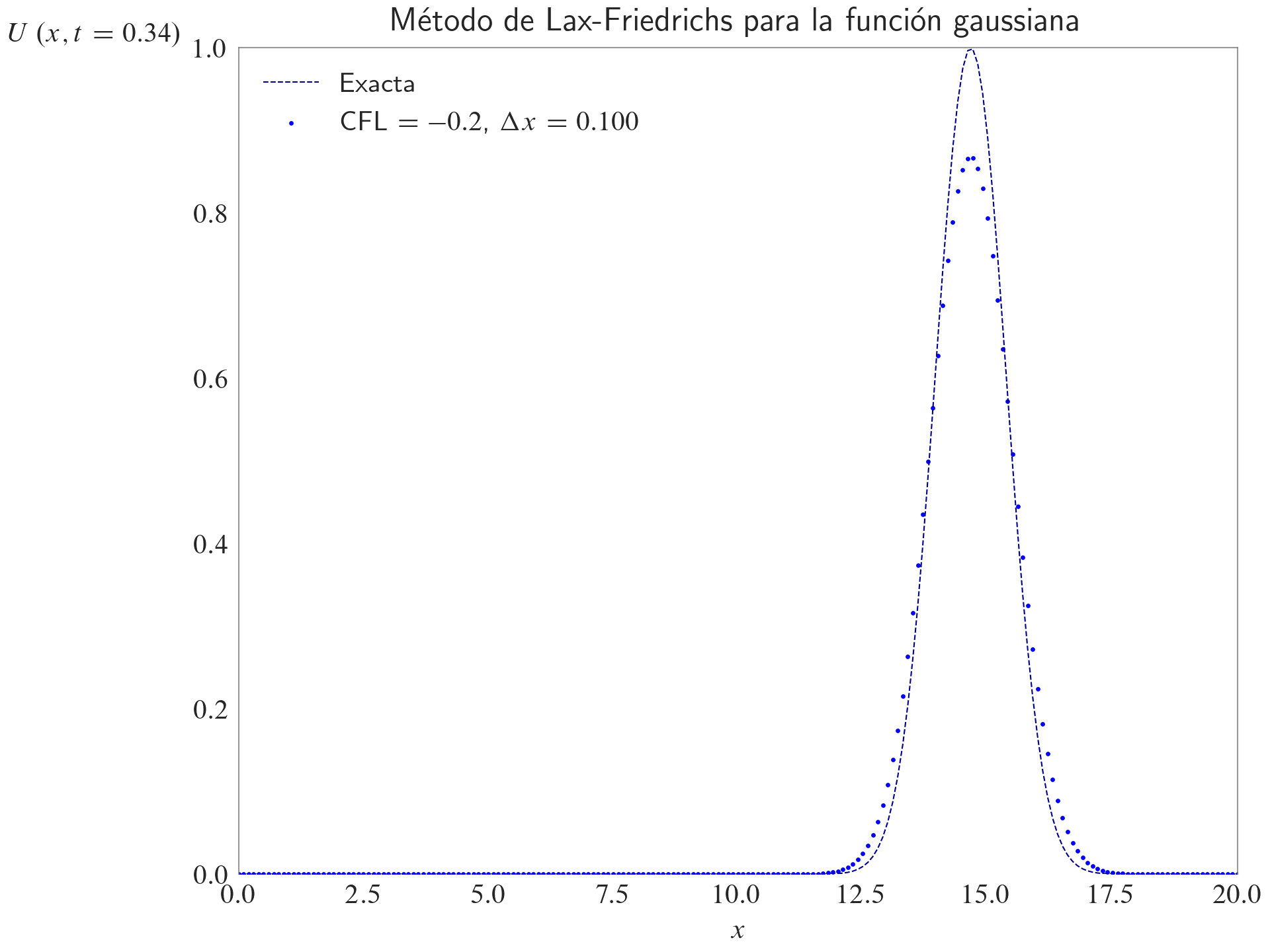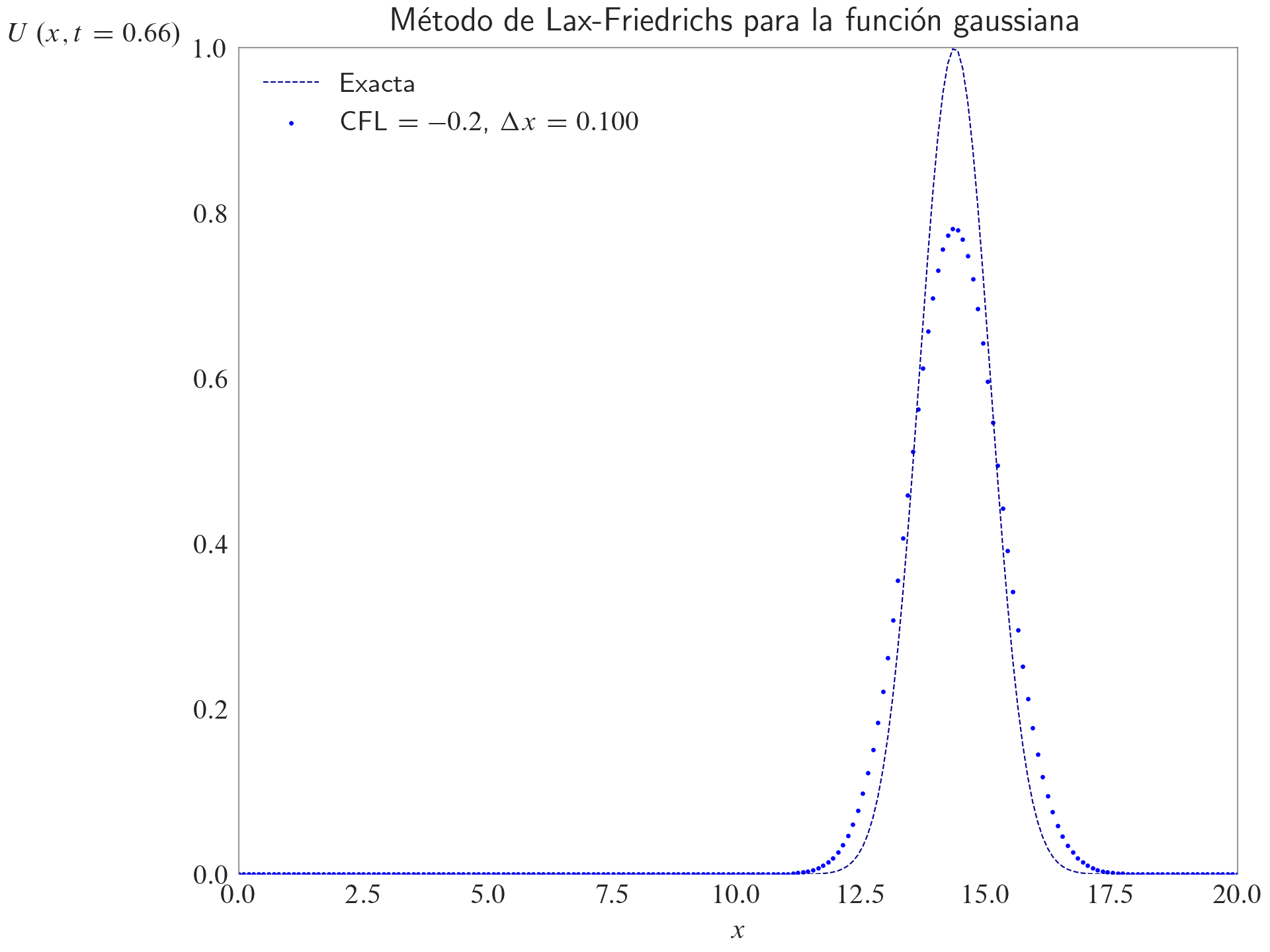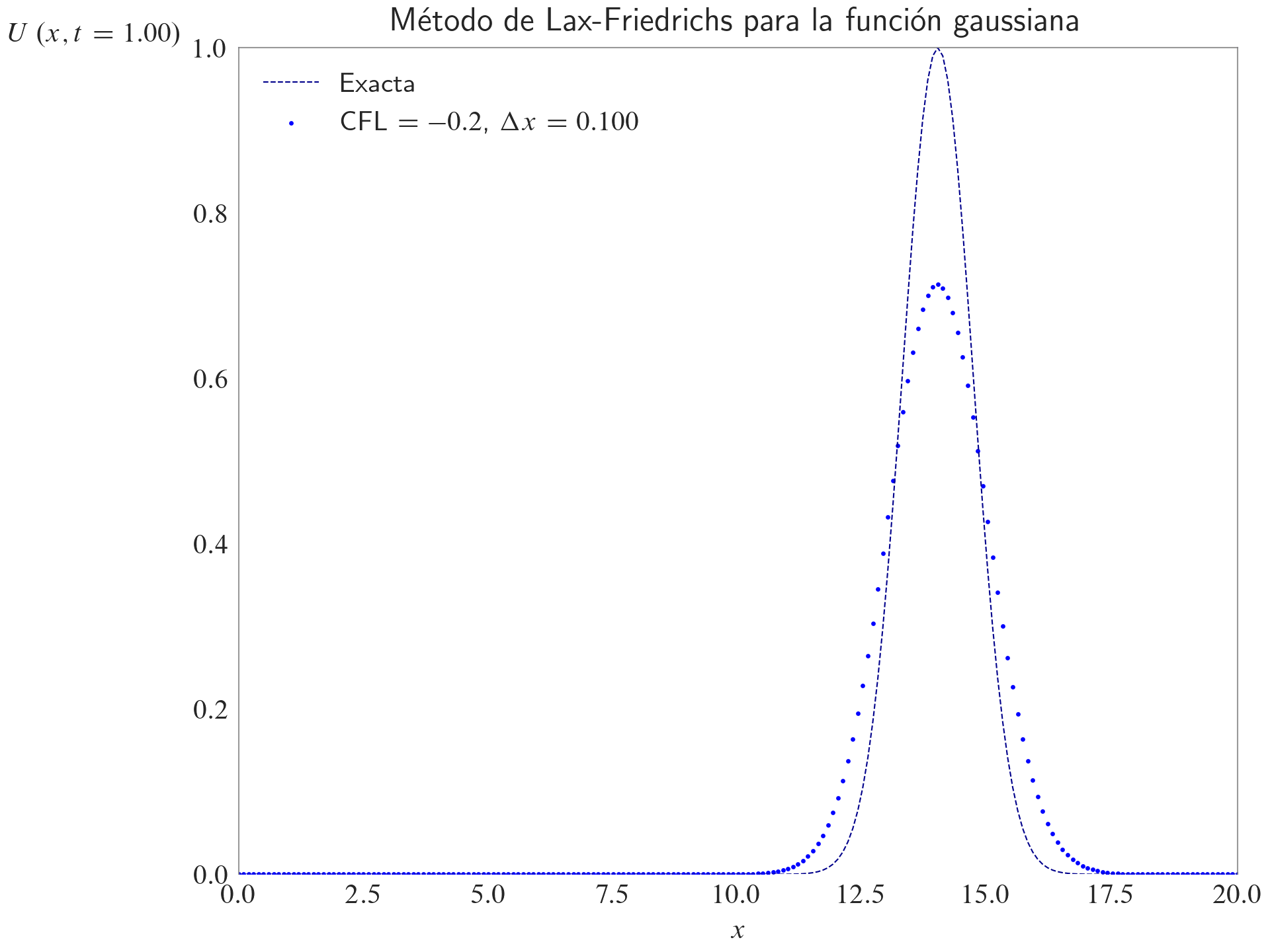
ax.set_title(label="Método de Lax-Friedrichs para la función gaussiana", loc="center")
ax.legend(loc="best")

U1 = U(x=x)


def init():
    ln.set_data(x, U(x))
    ln1.set_offsets(offsets=np.column_stack([x, U1]))

    return (ln,)


def update(frame):
    ln1.set_offsets(offsets=np.column_stack([x, U1]))
    ln.set_data(x, U(x=x - c * frame * Δt))
    U1[1:-1] = (
        0.5 * (np.roll(U1, -1) + np.roll(U1, 1))[1:-1]
        - 0.5 * cfl * (np.roll(U1, -1) - np.roll(U1, 1))[1:-1]
    )
    ax.set_ylabel(
        ylabel=rf"$U\left(x, t={frame * Δt:.2f}\right)$", loc="top", rotation=0
    )

    return (ln,)


anim = FuncAnimation(
    fig=fig,
    func=update,
    frames=tqdm(iterable=range(t.size), file=sys.stdout, colour="green"),
    interval=1,
    init_func=init,
    blit=True,
).save(
    filename="lax-friedrichsgaussiana.gif",
    writer=FFMpegWriter(
        fps=90,
        codec="libx265",
        metadata={
            "subject": "Numerical Analysis",
            "title": "Exact solution",
            "author": "Gloria Almozara Sainz",
            "genre": "Mathematics",
            "copyright": "2025",
            "srcform": "Matplotlib 3.9.3",
            "comment": "Numerical Simulation for advection PDE",
        },
    ),
    dpi=300,
    savefig_kwargs={"transparent": True, "facecolor": "none"},
)
plt.close()
Loading...

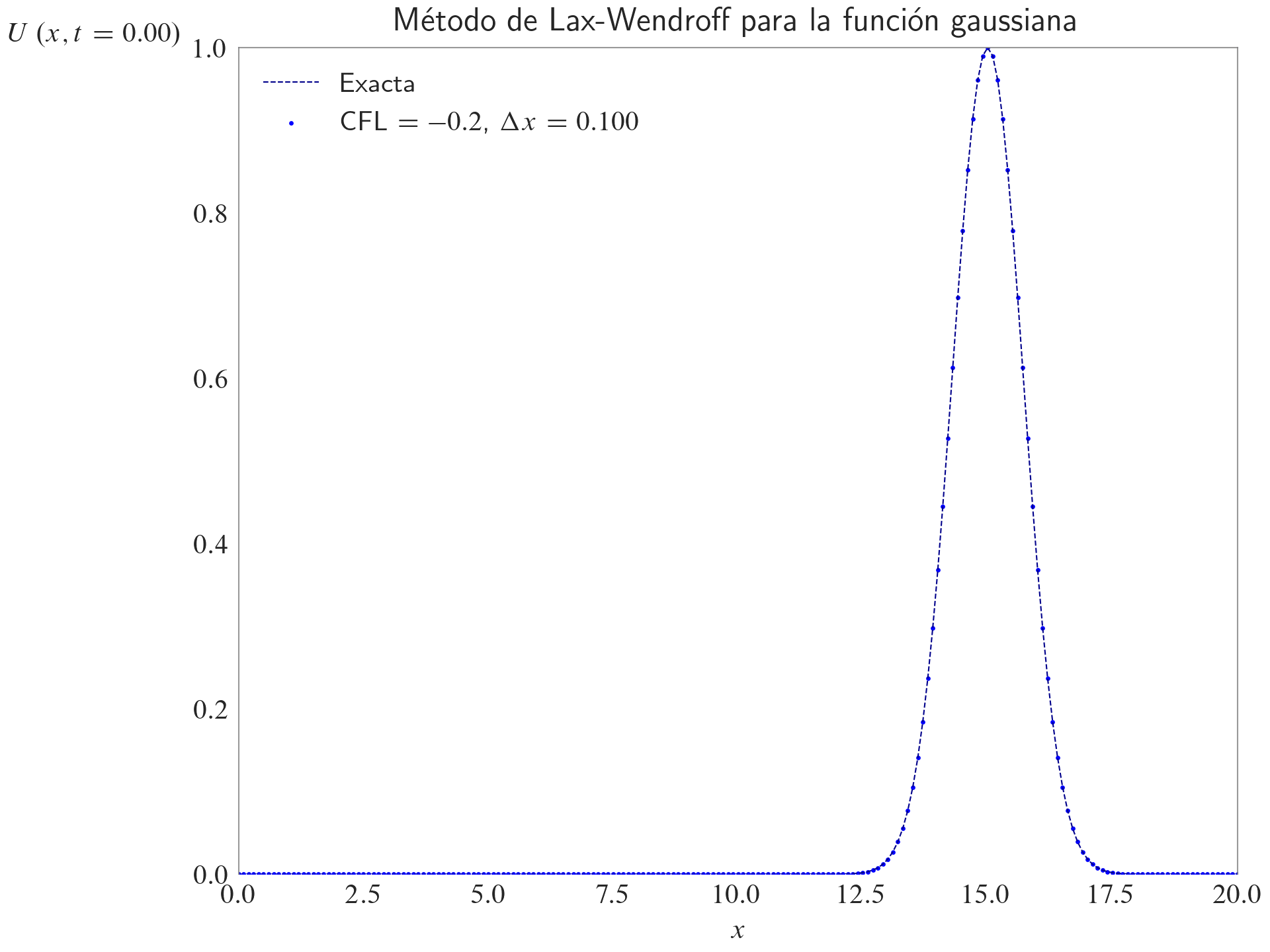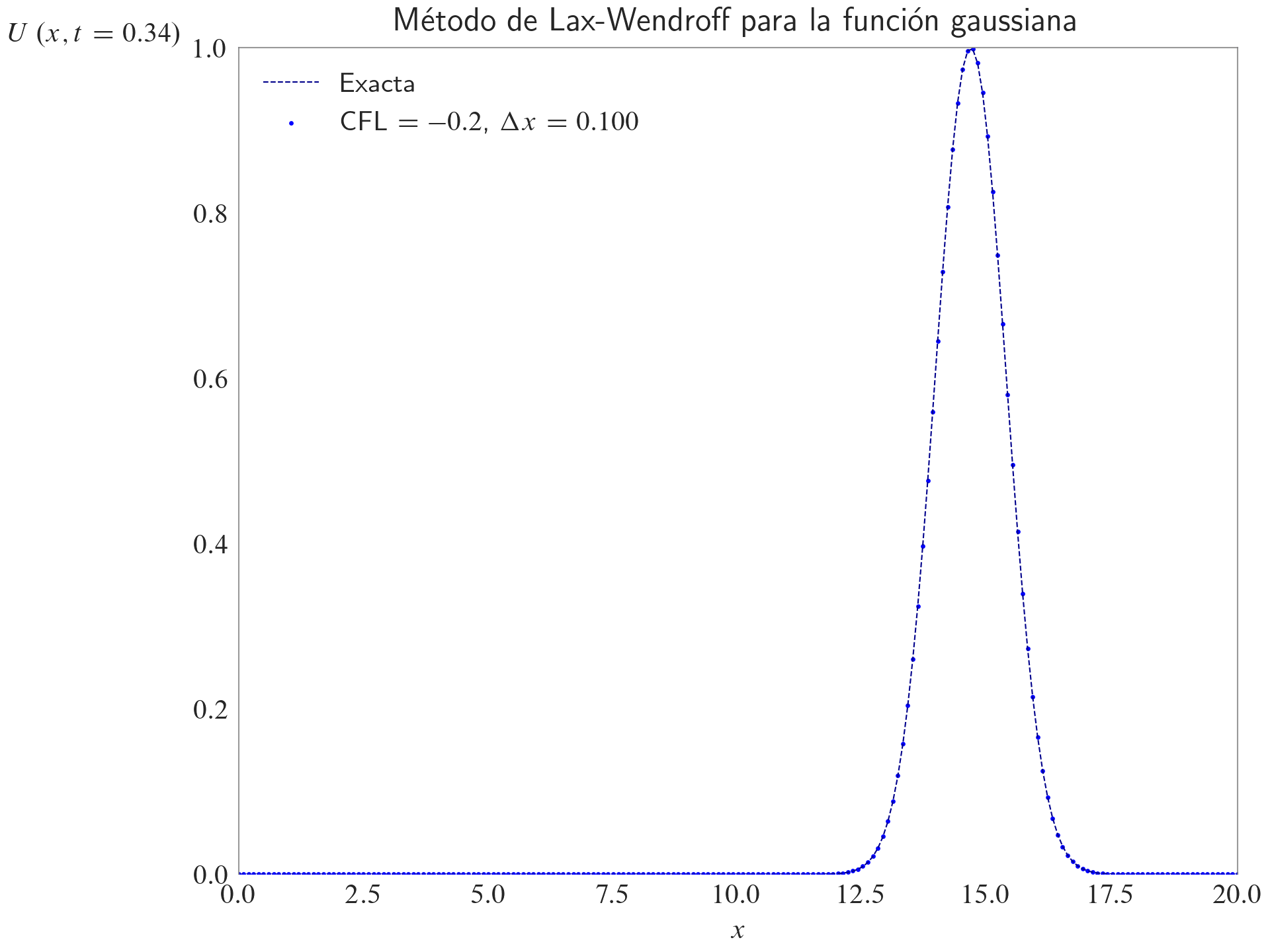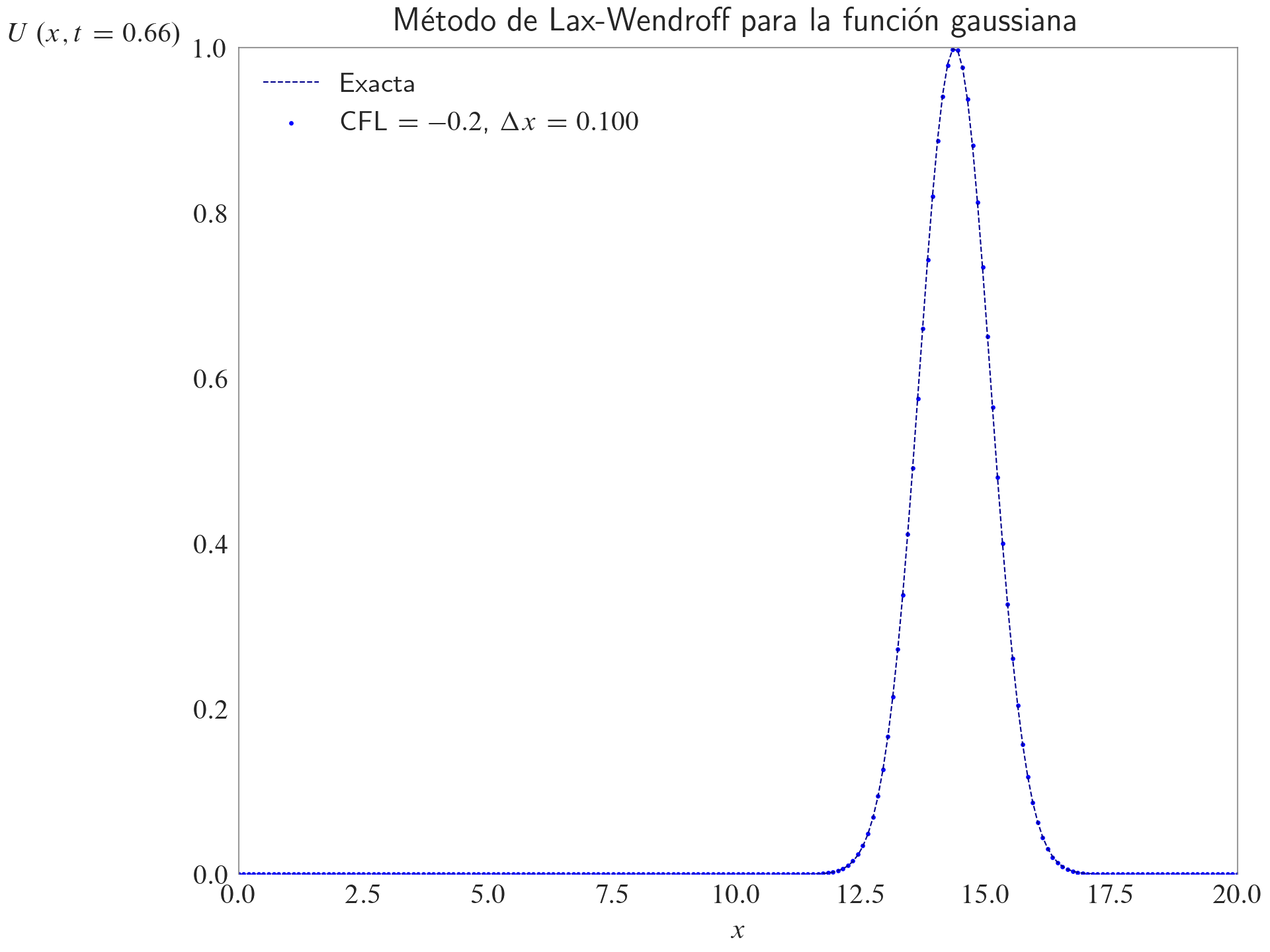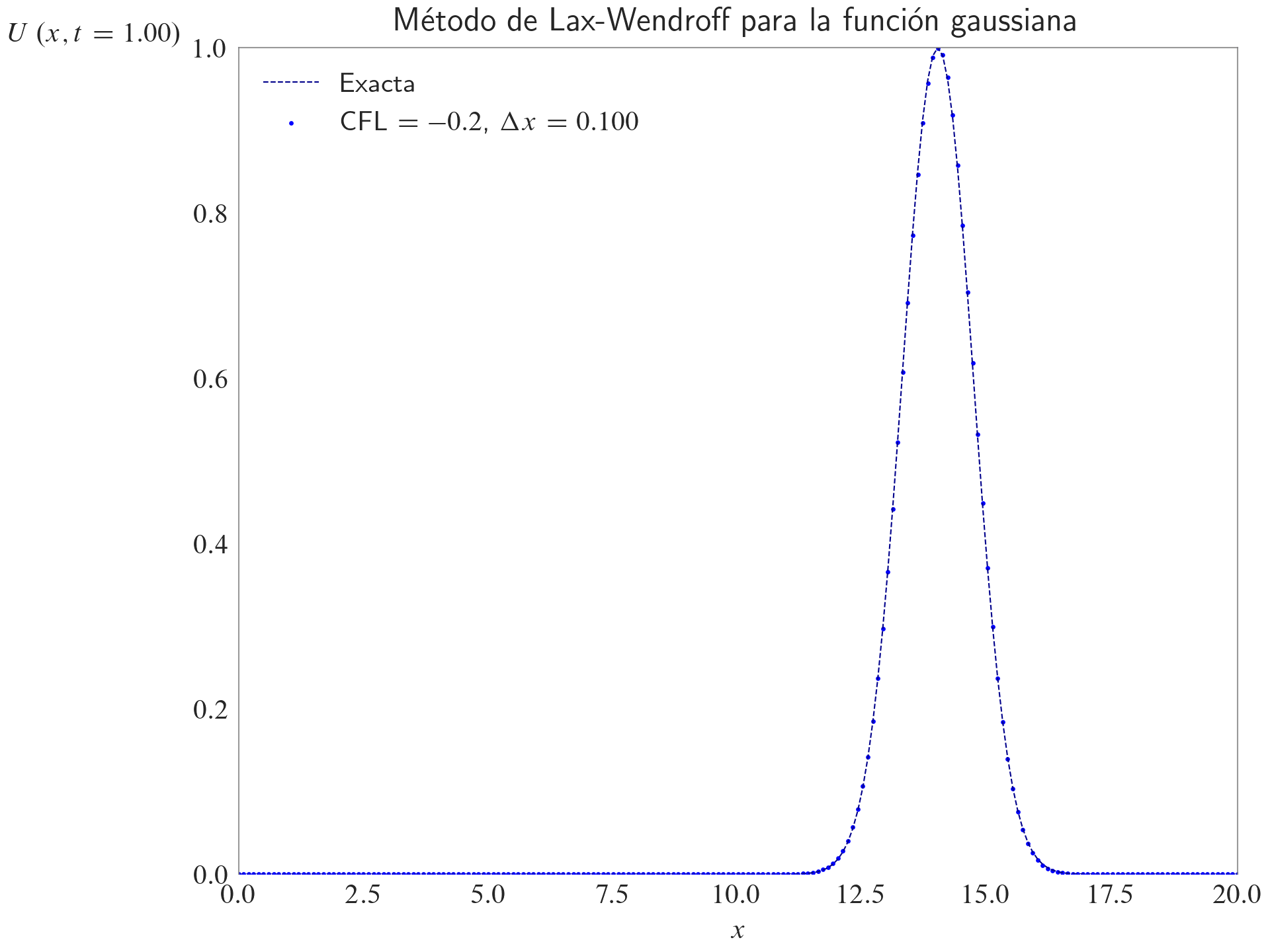
Método de Lax-Wendroff

Uin+1=Uin−cΔt2Δx(Ui+1n−Ui−1n)+c2Δt22Δx2(Ui+1n−2Uin+Ui−1n).U^{n+1}_{i}= U^{n}_{i}- c\frac{\Delta t}{2\Delta x} \left(U^{n}_{i+1}-U^{n}_{i-1}\right)+ c^{2} \frac{\Delta t^{2}}{2\Delta x^{2}} \left(U^{n}_{i+1}-2U^{n}_{i}+U^{n}_{i-1}\right).
(40)
fig, ax = plt.subplots(layout="constrained")

(ln,) = ax.plot(
    [],
    [],
    color="DarkBlue",
    label="Exacta",
    linestyle="dashed",
    linewidth=0.5,
)

ln1 = ax.scatter(
    x=[],
    y=[],
    c="blue",
    label=rf"CFL $={cfl:.1f}$, $\Delta x={Δx:.3f}$",
    s=0.4,
)
ax.spines["bottom"].set_color("none")
ax.spines["top"].set_alpha(alpha=0.8)
ax.spines["top"].set_edgecolor(color="gray")
ax.spines["top"].set_linewidth(w=0.5)
ax.spines["left"].set_alpha(alpha=0.8)
ax.spines["left"].set_edgecolor(color="gray")
ax.spines["left"].set_linewidth(w=0.5)
ax.spines["right"].set_alpha(alpha=0.8)
ax.spines["right"].set_edgecolor(color="gray")
ax.spines["right"].set_linewidth(w=0.5)
ax.set_xlabel(xlabel=r"$x$")
ax.set_xlim(left=x[0], right=x[-1])
ax.set_ylim(bottom=0, top=1)
ax.set_title(label="Método de Lax-Wendroff para la función gaussiana", loc="center")
ax.legend(loc="best")

U1 = U(x=x)


def init():
    ln.set_data(x, U(x))
    ln1.set_offsets(offsets=np.column_stack([x, U1]))

    return (ln,)


def update(frame):
    ln1.set_offsets(offsets=np.column_stack([x, U1]))
    ln.set_data(x, U(x=x - c * frame * Δt))
    U1[1:-1] -= (
        0.5 * cfl * (np.roll(U1, -1) - np.roll(U1, 1))[1:-1]
        - 0.5 * cfl**2 * (np.roll(U1, -1) - 2 * U1 + np.roll(U1, 1))[1:-1]
    )
    ax.set_ylabel(
        ylabel=rf"$U\left(x, t={frame * Δt:.2f}\right)$", loc="top", rotation=0
    )

    return (ln,)


anim = FuncAnimation(
    fig=fig,
    func=update,
    frames=tqdm(iterable=range(t.size), file=sys.stdout, colour="green"),
    interval=1,
    init_func=init,
    blit=True,
).save(
    filename="lax-wendroffgaussiana.gif",
    writer=FFMpegWriter(
        fps=90,
        codec="libx265",
        metadata={
            "subject": "Numerical Analysis",
            "title": "Exact solution",
            "author": "Gloria Almozara Sainz",
            "genre": "Mathematics",
            "copyright": "2025",
            "srcform": "Matplotlib 3.9.3",
            "comment": "Numerical Simulation for advection PDE",
        },
    ),
    dpi=300,
    savefig_kwargs={"transparent": True, "facecolor": "none"},
)
plt.close()
Loading...

Ejemplo 2

Ω=[0,30]\Omega=\left[0,30\right], Δx=0.12\Delta x=0.12, Δt=0.02\Delta t=0.02, c=1c=1.

U0(x)={2, si x<15,1, si x>15.U_{0}\left(x\right)= \begin{cases} 2, & \text{ si }x<15,\\ 1, & \text{ si }x>15. \end{cases}
(41)
x, Δx = np.linspace(start=0, stop=30, num=251, retstep=True)
t, Δt = np.linspace(start=0, stop=1, num=51, retstep=True)
c = 1
cfl = c * Δt / Δx
def U(x, U_left=2, U_right=1, x0=15):
    return U_left + (U_right - U_left) * np.heaviside(x - x0, 0)
fig, ax = plt.subplots(layout="constrained")
ax.plot(
    x,
    U(x),
    color="red",
    label=r"$U_{0}\left(x\right)$",
    linestyle="solid",
    linewidth=1.0,
)
ax.spines["bottom"].set_color("none")
ax.spines["top"].set_color("none")
ax.spines["left"].set_alpha(alpha=0.8)
ax.spines["left"].set_edgecolor(color="gray")
ax.spines["left"].set_linewidth(w=0.5)
ax.spines["right"].set_alpha(alpha=0.8)
ax.spines["right"].set_edgecolor(color="gray")
ax.spines["right"].set_linewidth(w=0.5)
ax.set_title(label=r"Condición inicial $U_{0}=2-H\left(x-15\right)$", loc="center")
ax.set_xlim(left=x[0], right=x[-1])
ax.set_ylim(bottom=U(x).min(), top=U(x).max())
ax.legend(loc="best")
Loading...
fig, ax = plt.subplots(layout="constrained")
(ln,) = ax.plot(
    [],
    [],
    color="red",
    label="Exacta",
    linestyle="dashed",
    linewidth=0.5,
)
ax.spines["bottom"].set_color("none")
ax.spines["top"].set_color("none")
ax.spines["left"].set_alpha(alpha=0.8)
ax.spines["left"].set_edgecolor(color="gray")
ax.spines["left"].set_linewidth(w=0.5)
ax.spines["right"].set_alpha(alpha=0.8)
ax.spines["right"].set_edgecolor(color="gray")
ax.spines["right"].set_linewidth(w=0.5)
ax.set_xlabel(xlabel=r"$x$")
ax.set_xlim(left=x[0], right=x[-1])
ax.set_ylim(bottom=U(x).min(), top=U(x).max())
ax.set_title(label=r"Solución exacta $u\left(x,t\right)=u(x-ct)$")
ax.legend(loc="best")

def init():
    ln.set_data(x, U(x))

    return (ln,)


def update(frame):
    ln.set_data(x, U(x=x - c * (t[0] + frame * Δt)))
    ax.set_ylabel(
        ylabel=rf"$U\left(x, t={frame * Δt:.2f}\right)$", loc="top", rotation=0
    )

    return (ln,)


anim = FuncAnimation(
    fig=fig,
    func=update,
    frames=tqdm(iterable=range(t.size), file=sys.stdout, colour="green"),
    interval=1,
    init_func=init,
    blit=True,
).save(
    filename="exactheaviside.gif",
    writer=FFMpegWriter(
        fps=90,
        codec="libx265",
        metadata={
            "subject": "Numerical Analysis",
            "title": "Exact solution",
            "author": "Gloria Almozara Sainz",
            "genre": "Mathematics",
            "copyright": "2025",
            "srcform": "Matplotlib 3.9.3",
            "comment": "Numerical Simulation for advection PDE",
        },
    ),
    dpi=300,
    savefig_kwargs={"transparent": True, "facecolor": "none"},
)
plt.close()
Loading...

Método Upwind

Uin+1=Uin−cΔtΔx(Uin−Ui−1n).U^{n+1}_{i}= U^{n}_{i}- \frac{c\Delta t}{\Delta x} \left(U^{n}_{i}-U^{n}_{i-1}\right).
(42)
fig, ax = plt.subplots(layout="constrained")

(ln,) = ax.plot(
    [],
    [],
    color="DarkBlue",
    label="Exacta",
    linestyle="dashed",
    linewidth=0.5,
)
ln1 = ax.scatter(
    x=[],
    y=[],
    c="blue",
    label=rf"CFL $={cfl:.1f}$, $\Delta x={Δx:.3f}$",
    s=0.4,
)
ax.spines["bottom"].set_color("none")
ax.spines["top"].set_color("none")
ax.spines["left"].set_alpha(alpha=0.8)
ax.spines["left"].set_edgecolor(color="gray")
ax.spines["left"].set_linewidth(w=0.5)
ax.spines["right"].set_alpha(alpha=0.8)
ax.spines["right"].set_edgecolor(color="gray")
ax.spines["right"].set_linewidth(w=0.5)
ax.set_xlabel(xlabel=r"$x$")
ax.set_xlim(left=x[0], right=x[-1])
ax.set_ylim(bottom=U(x).min(), top=U(x).max())
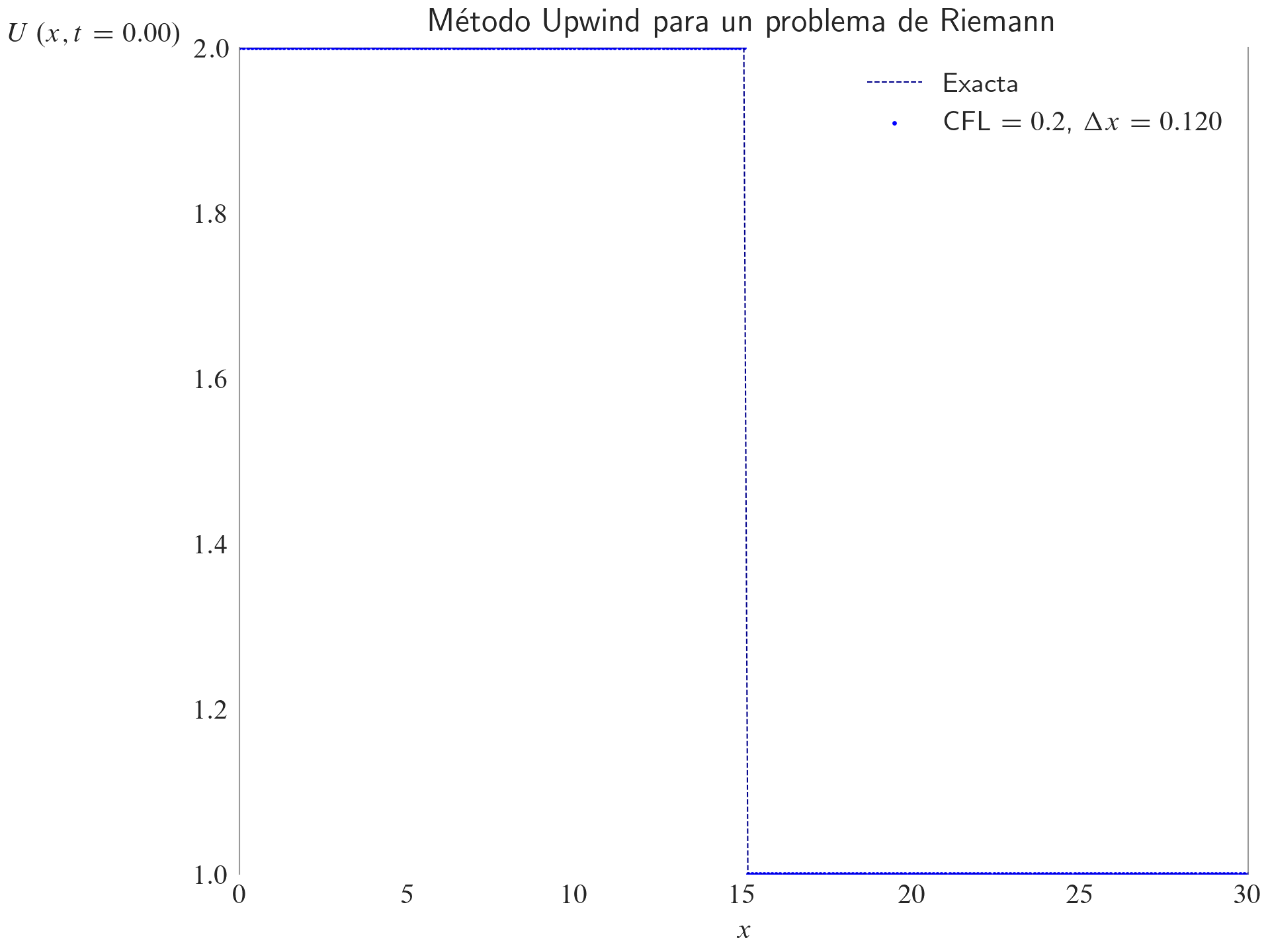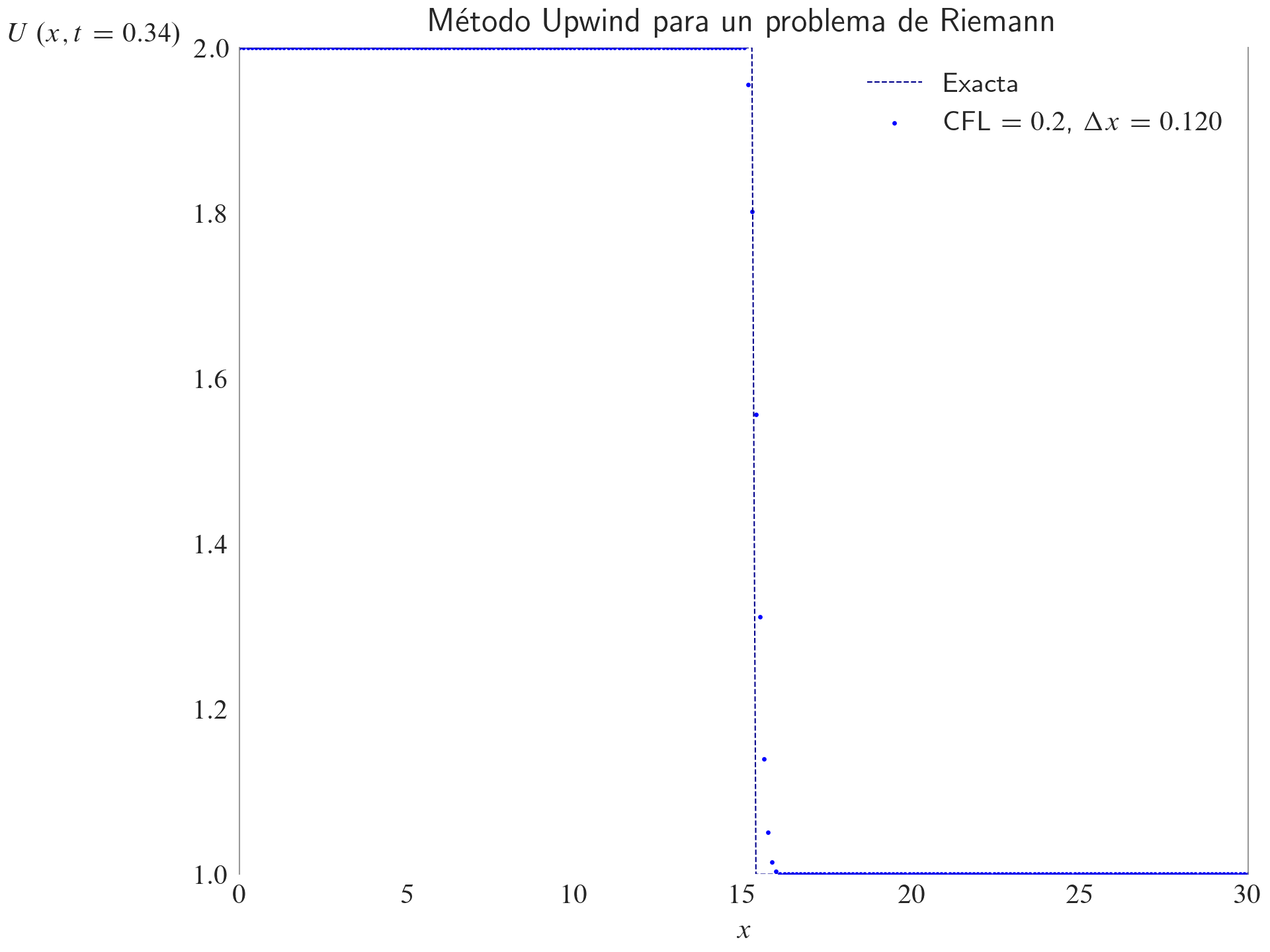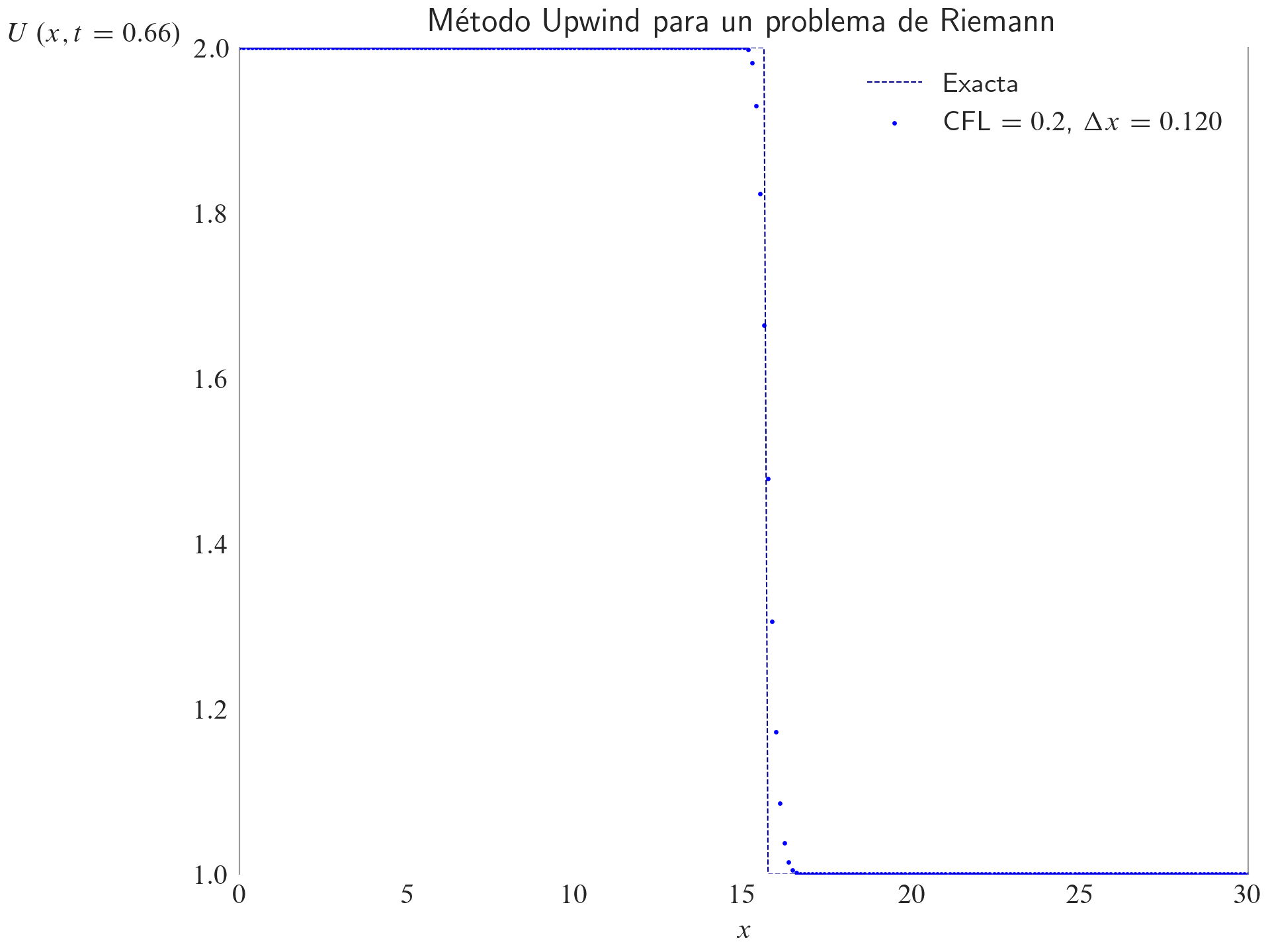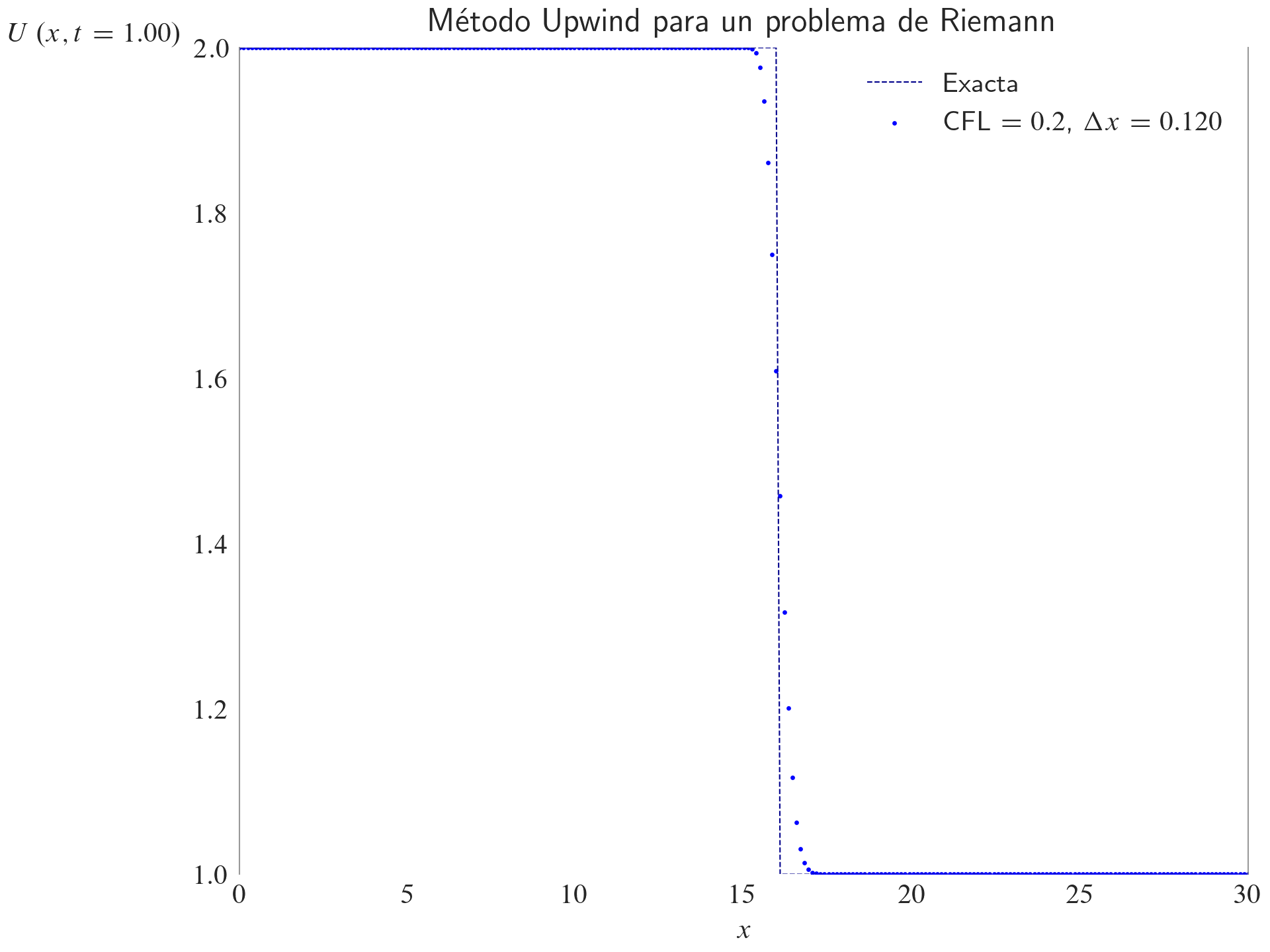
ax.set_title(label="Método Upwind para un problema de Riemann", loc="center")
ax.legend(loc="best")

U1 = U(x=x)


def init():
    ln.set_data(x, U(x))
    ln1.set_offsets(offsets=np.column_stack([x, U1]))

    return (ln,)


def update(frame):
    ln1.set_offsets(offsets=np.column_stack([x, U1]))
    ln.set_data(x, U(x=x - c * frame * Δt))
    U1[1:] -= cfl * (U1 - np.roll(U1, 1))[1:]
    ax.set_ylabel(
        ylabel=rf"$U\left(x, t={frame * Δt:.2f}\right)$", loc="top", rotation=0
    )

    return (ln,)


anim = FuncAnimation(
    fig=fig,
    func=update,
    frames=tqdm(iterable=range(t.size), file=sys.stdout, colour="green"),
    interval=1,
    init_func=init,
    blit=True,
).save(
    filename="upwindheaviside.gif",
    writer=FFMpegWriter(
        fps=90,
        codec="libx265",
        metadata={
            "subject": "Numerical Analysis",
            "title": "Exact solution",
            "author": "Gloria Almozara Sainz",
            "genre": "Mathematics",
            "copyright": "2025",
            "srcform": "Matplotlib 3.9.3",
            "comment": "Numerical Simulation for advection PDE",
        },
    ),
    dpi=300,
    savefig_kwargs={"transparent": True, "facecolor": "none"},
)
plt.close()
Loading...
fig, ax = plt.subplots(layout="constrained")

(ln,) = ax.plot(
    [],
    [],
    color="DarkBlue",
    label="Exacta",
    linestyle="dashed",
    linewidth=0.5,
)
ln1 = ax.scatter(
    x=[],
    y=[],
    c="blue",
    label=rf"CFL $={cfl:.1f}$, $\Delta x={Δx:.3f}$",
    s=0.4,
)
ax.spines["bottom"].set_color("none")
ax.spines["top"].set_color("none")
ax.spines["left"].set_alpha(alpha=0.8)
ax.spines["left"].set_edgecolor(color="gray")
ax.spines["left"].set_linewidth(w=0.5)
ax.spines["right"].set_alpha(alpha=0.8)
ax.spines["right"].set_edgecolor(color="gray")
ax.spines["right"].set_linewidth(w=0.5)
ax.set_xlabel(xlabel=r"$x$")
ax.set_xlim(left=x[0], right=x[-1])
ax.set_ylim(bottom=U(x).min(), top=U(x).max())
ax.set_title(label="Método de Lax-Friedrichs para un problema de Riemann", loc="center")
ax.legend(loc="best")

U1 = U(x=x)


def init():
    ln.set_data(x, U(x))
    ln1.set_offsets(offsets=np.column_stack([x, U1]))

    return (ln,)


def update(frame):
    ln1.set_offsets(offsets=np.column_stack([x, U1]))
    ln.set_data(x, U(x=x - c * frame * Δt))
    U1[1:-1] = (
        0.5 * (np.roll(U1, -1) + np.roll(U1, 1))[1:-1]
        - 0.5 * cfl * (np.roll(U1, -1) - np.roll(U1, 1))[1:-1]
    )
    ax.set_ylabel(
        ylabel=rf"$U\left(x, t={frame * Δt:.2f}\right)$", loc="top", rotation=0
    )

    return (ln,)


anim = FuncAnimation(
    fig=fig,
    func=update,
    frames=tqdm(iterable=range(t.size), file=sys.stdout, colour="green"),
    interval=1,
    init_func=init,
    blit=True,
).save(
    filename="lax-friedrichsheaviside.gif",
    writer=FFMpegWriter(
        fps=90,
        codec="libx265",
        metadata={
            "subject": "Numerical Analysis",
            "title": "Exact solution",
            "author": "Gloria Almozara Sainz",
            "genre": "Mathematics",
            "copyright": "2025",
            "srcform": "Matplotlib 3.9.3",
            "comment": "Numerical Simulation for advection PDE",
        },
    ),
    dpi=300,
    savefig_kwargs={"transparent": True, "facecolor": "none"},
)
plt.close()
Loading...
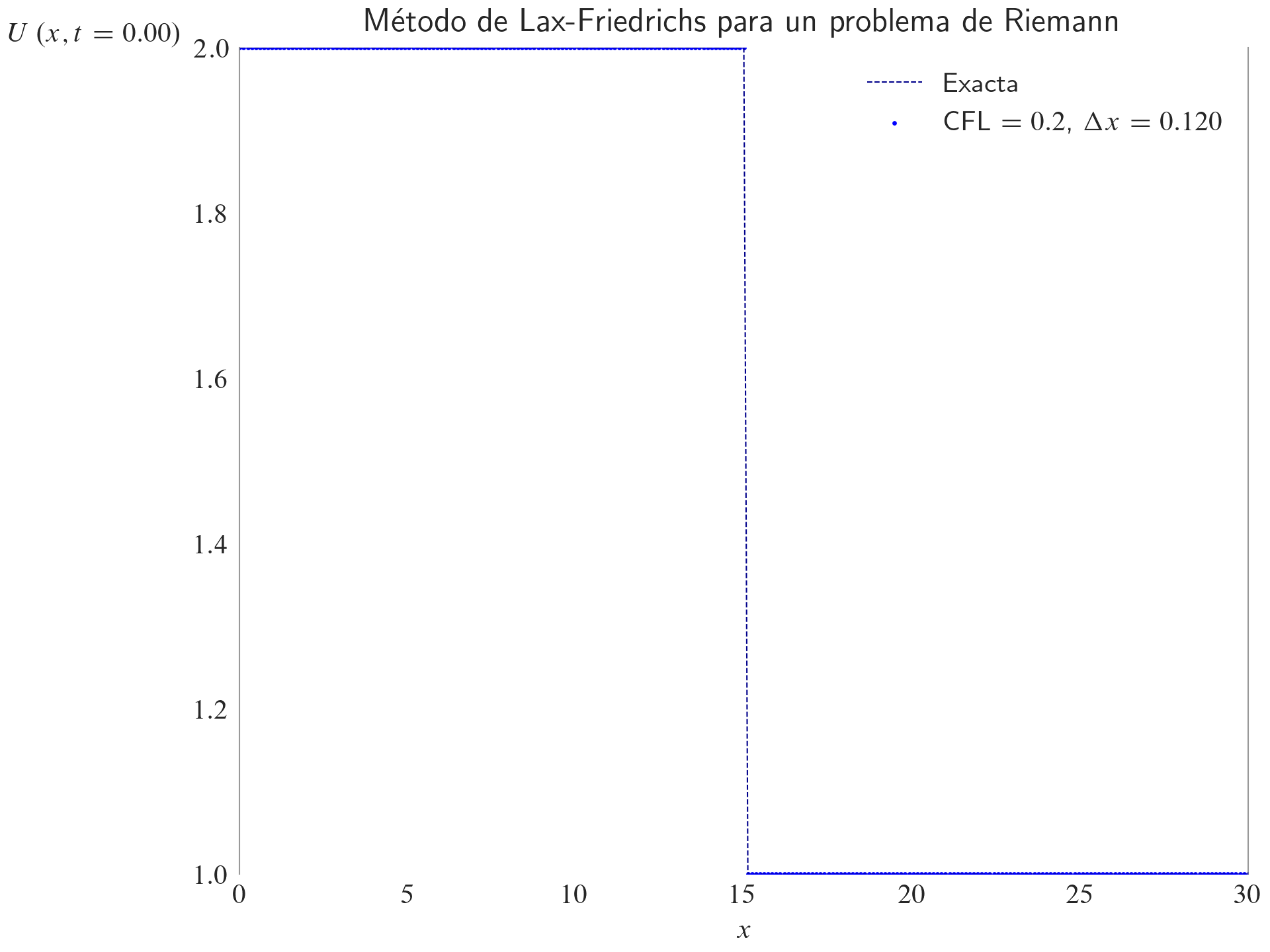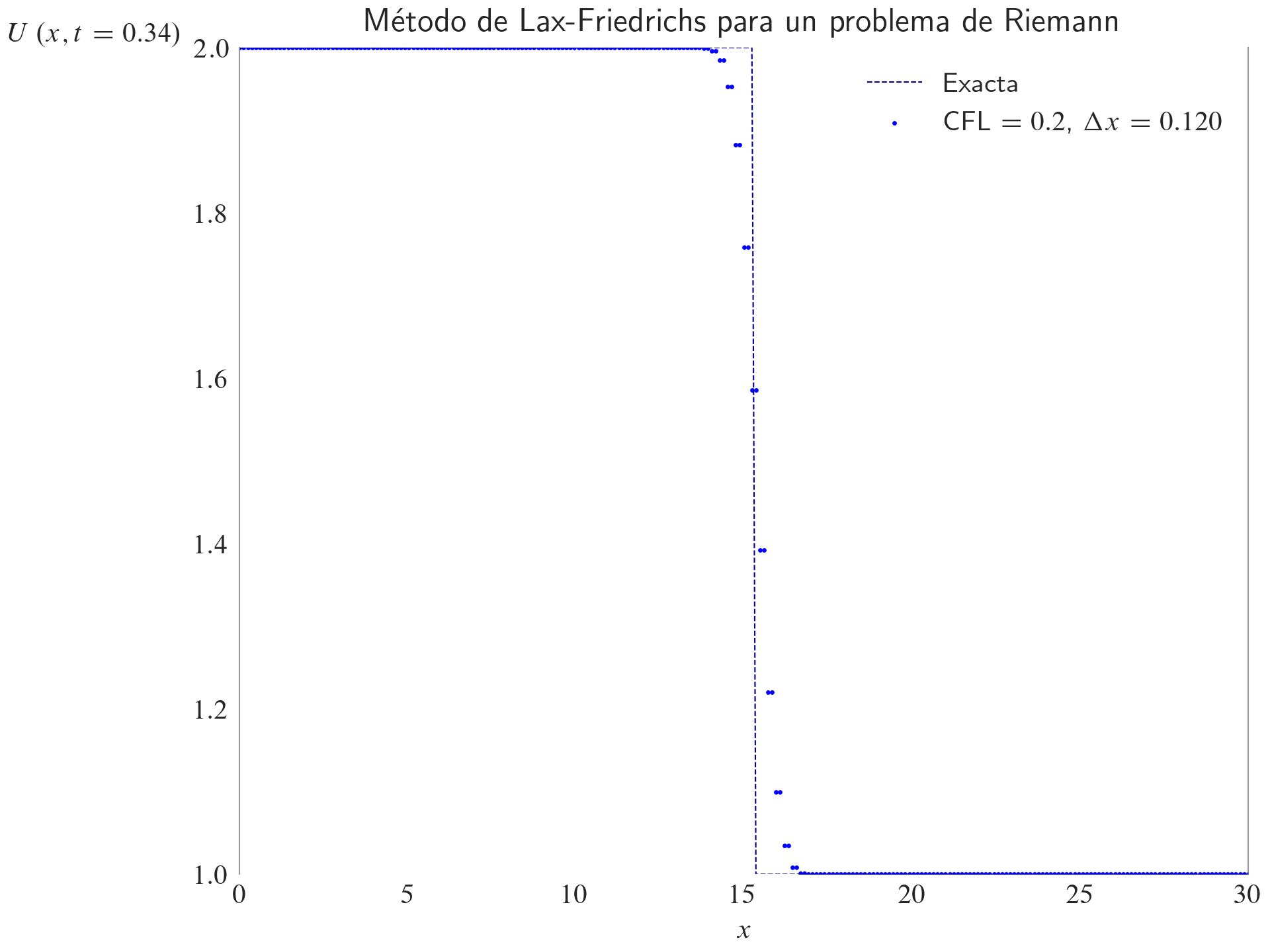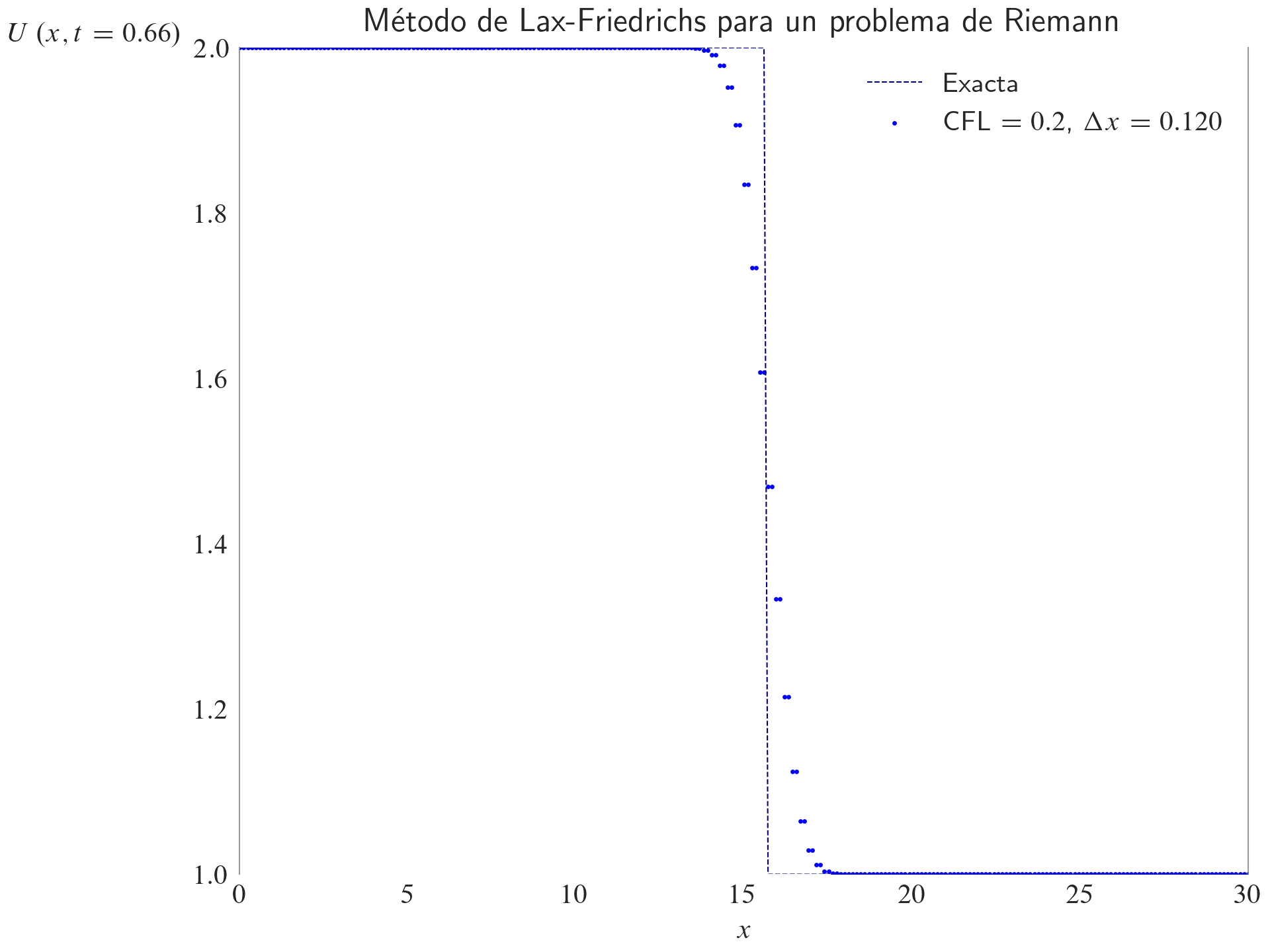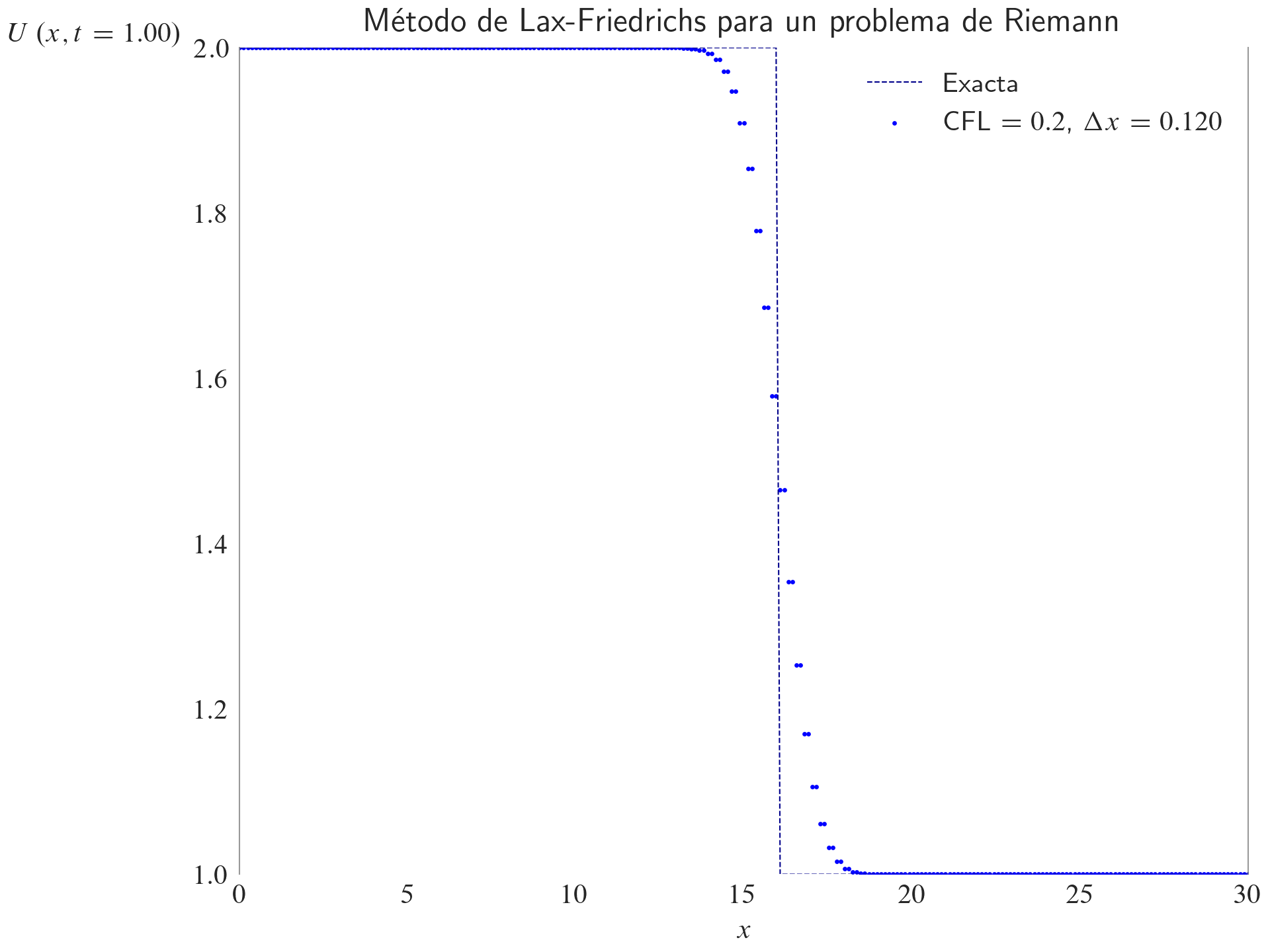
fig, ax = plt.subplots(layout="constrained")

(ln,) = ax.plot(
    [],
    [],
    color="DarkBlue",
    label="Exacta",
    linestyle="dashed",
    linewidth=0.5,
)
ln1 = ax.scatter(
    x=[],
    y=[],
    c="blue",
    label=rf"CFL $={cfl:.1f}$, $\Delta x={Δx:.3f}$",
    s=0.4,
)
ax.spines["bottom"].set_color("none")
ax.spines["top"].set_color("none")
ax.spines["left"].set_alpha(alpha=0.8)
ax.spines["left"].set_edgecolor(color="gray")
ax.spines["left"].set_linewidth(w=0.5)
ax.spines["right"].set_alpha(alpha=0.8)
ax.spines["right"].set_edgecolor(color="gray")
ax.spines["right"].set_linewidth(w=0.5)
ax.set_xlabel(xlabel=r"$x$")
ax.set_xlim(left=x[0], right=x[-1])
ax.set_ylim(bottom=U(x).min() - 0.01, top=U(x).max() + 0.01)
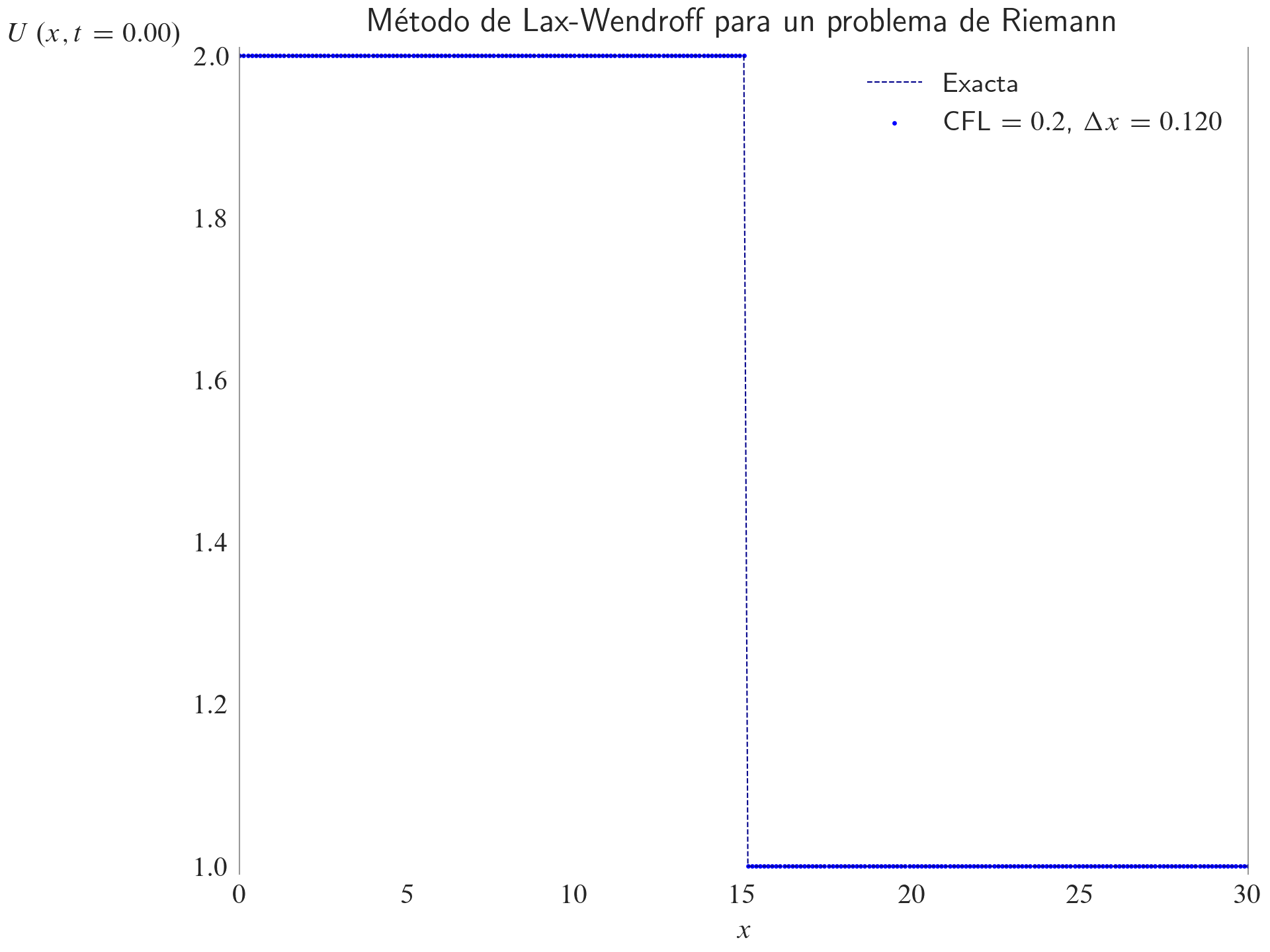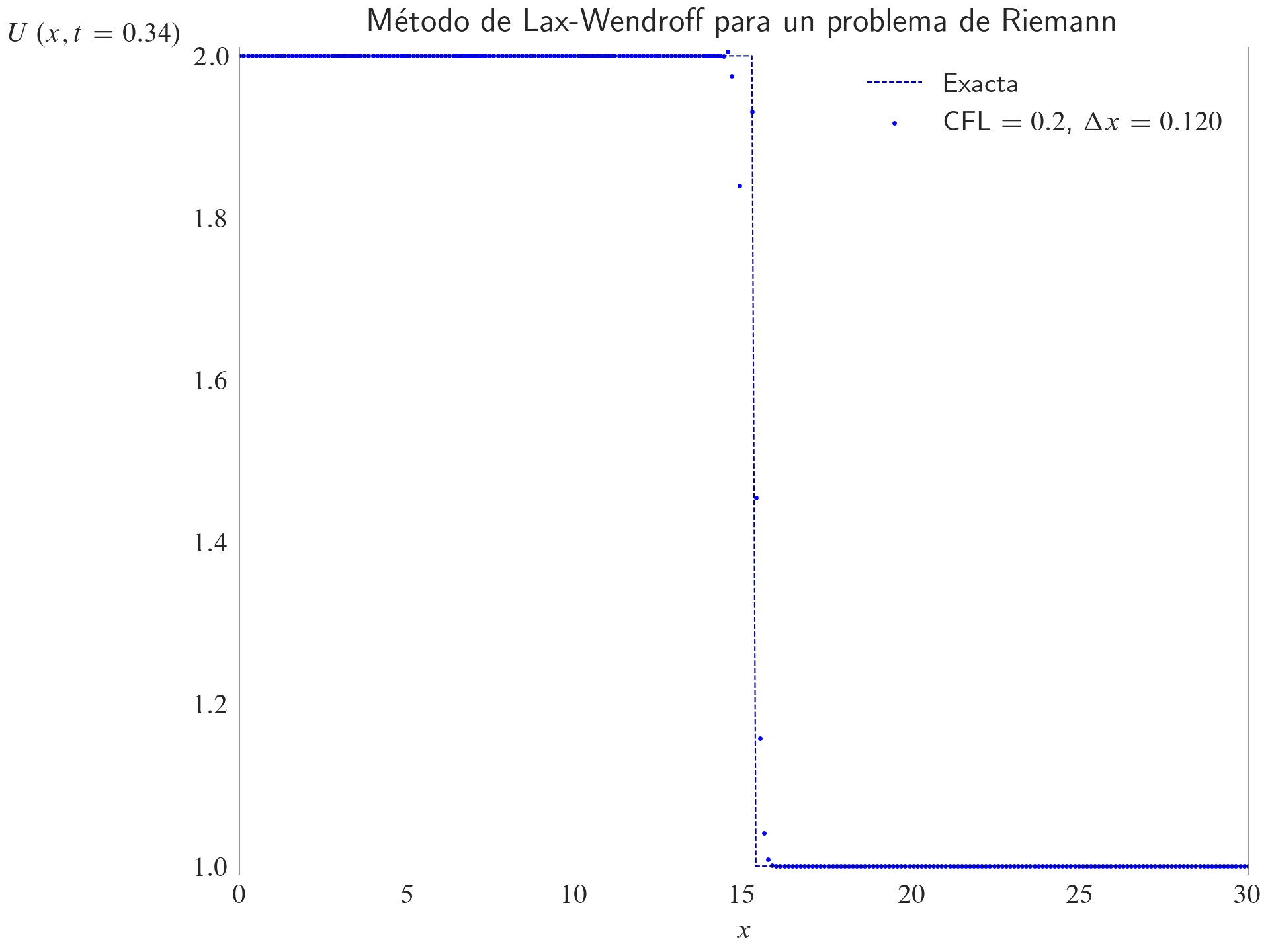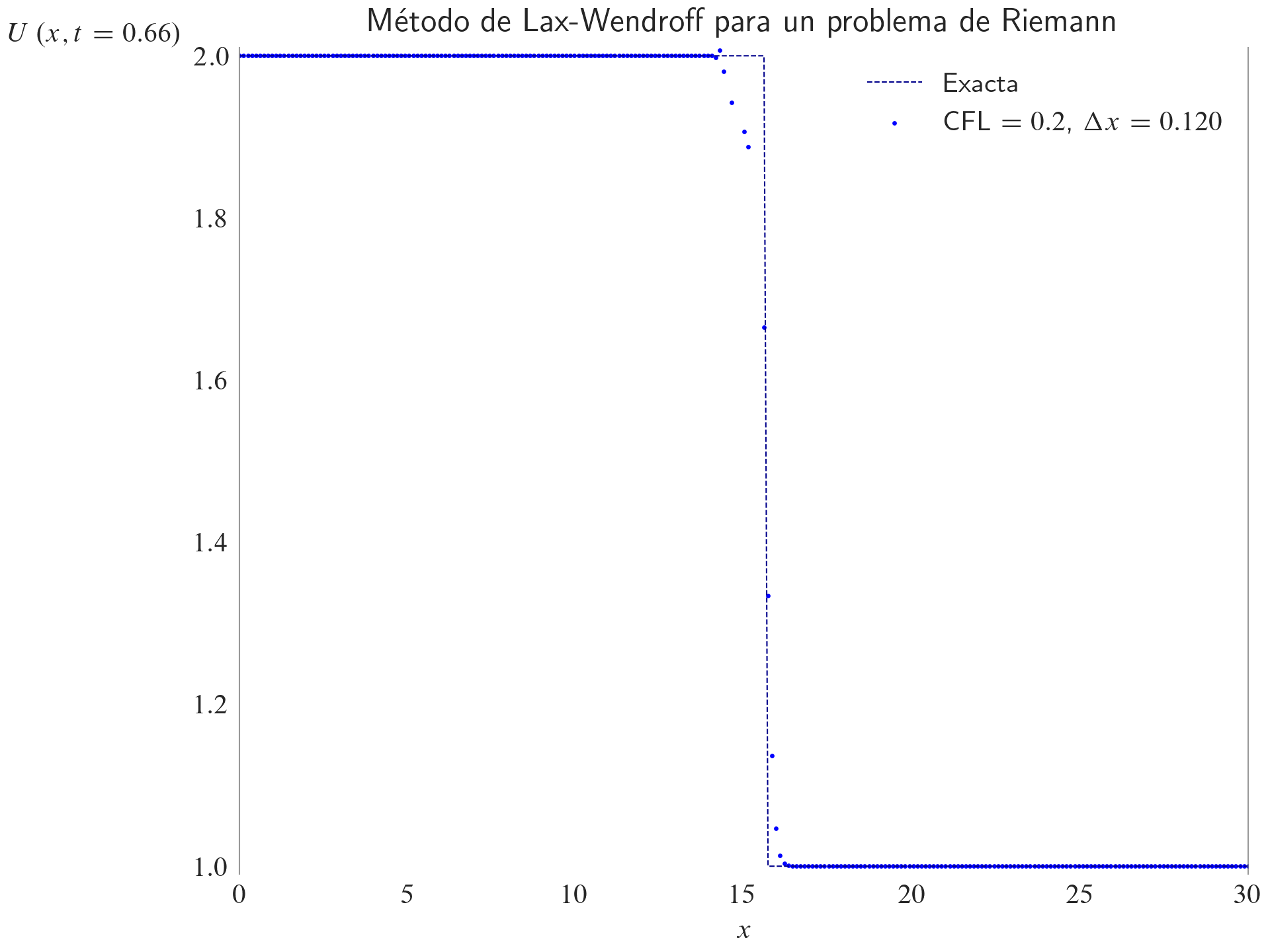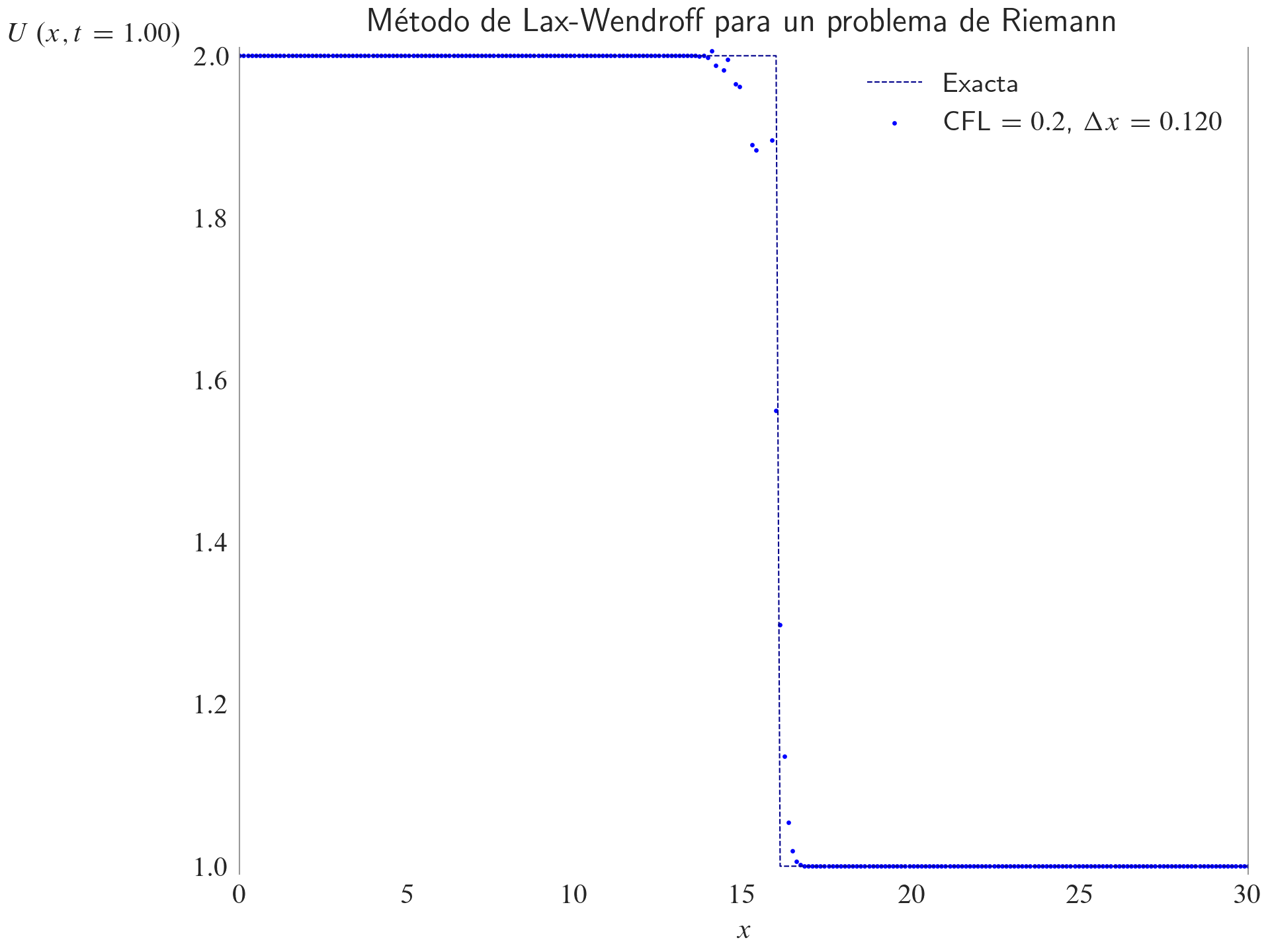
ax.set_title(label="Método de Lax-Wendroff para un problema de Riemann", loc="center")
ax.legend(loc="best")

U1 = U(x=x)


def init():
    ln.set_data(x, U(x))
    ln1.set_offsets(offsets=np.column_stack([x, U1]))

    return (ln,)


def update(frame):
    ln1.set_offsets(offsets=np.column_stack([x, U1]))
    ln.set_data(x, U(x=x - c * frame * Δt))
    U1[1:-1] -= (
        0.5 * cfl * (np.roll(U1, -1) - np.roll(U1, 1))[1:-1]
        - 0.5 * cfl**2 * (np.roll(U1, -1) - 2 * U1 + np.roll(U1, 1))[1:-1]
    )
    ax.set_ylabel(
        ylabel=rf"$U\left(x, t={frame * Δt:.2f}\right)$", loc="top", rotation=0
    )

    return (ln,)


anim = FuncAnimation(
    fig=fig,
    func=update,
    frames=tqdm(iterable=range(t.size), file=sys.stdout, colour="green"),
    interval=1,
    init_func=init,
    blit=True,
).save(
    filename="lax-wendroffheaviside.gif",
    writer=FFMpegWriter(
        fps=90,
        codec="libx265",
        metadata={
            "subject": "Numerical Analysis",
            "title": "Exact solution",
            "author": "Gloria Almozara Sainz",
            "genre": "Mathematics",
            "copyright": "2025",
            "srcform": "Matplotlib 3.9.3",
            "comment": "Numerical Simulation for advection PDE",
        },
    ),
    dpi=300,
    savefig_kwargs={"transparent": True, "facecolor": "none"},
)
plt.close()
Loading...

Ejemplo 3

vt+cg(x)vx=0,x∈[0,1],t∈[0,T]ut+cn(x)ux=0,x∈[0,1],t∈[0,T]v(x,0)=1u(x,0)=0.7\begin{aligned} v_t + c_g\left(x\right)v_{x} &= 0,\quad x\in\left[0,1\right],\quad t\in\left[0,T\right] \\ u_t + c_n\left(x\right)u_{x} &= 0,\quad x\in\left[0,1\right],\quad t\in\left[0,T\right] \\ v\left(x,0\right)&=1\\ u\left(x,0\right)&=0.7 \end{aligned}
(43)

Ω=[0,1]\Omega=\left[0,1\right], Δx=0.025\Delta x=0.025, Δt=0.0005\Delta t=0.0005, Nt=300N_{t}=300

x, Δx = np.linspace(start=0, stop=1, num=41, retstep=True)
t, Δt = np.linspace(start=0, stop=0.15, num=301, retstep=True)
def U(x):
    return np.exp(-np.power(x - 15, 2))
def V(x):
    return np.exp(-np.power(x - 15, 2)) + 2
fig, ax = plt.subplots(layout="constrained")
ax.plot(
    x,
    U(x),
    color="red",
    label=r"$U_{0}\left(x\right)$",
    linestyle="solid",
    linewidth=1.0,
)
ax.plot(
    x,
    V(x),
    color="red",
    label=r"$V_{0}\left(x\right)$",
    linestyle="solid",
    linewidth=1.0,
)
ax.spines["bottom"].set_color("none")
ax.spines["top"].set_alpha(alpha=0.8)
ax.spines["top"].set_edgecolor(color="gray")
ax.spines["top"].set_linewidth(w=0.5)
ax.spines["left"].set_alpha(alpha=0.8)
ax.spines["left"].set_edgecolor(color="gray")
ax.spines["left"].set_linewidth(w=0.5)
ax.spines["right"].set_alpha(alpha=0.8)
ax.spines["right"].set_edgecolor(color="gray")
ax.spines["right"].set_linewidth(w=0.5)
# ax.set_xlim(left=x[0], right=x[-1])
# ax.set_ylim(bottom=0, top=1)
ax.set_title(
    label=r"Condición inicial $U_{0}\left(x\right)=e^{-{\left(x-15\right)}^{2}}$",
    loc="center",
)
ax.legend(loc="best")
Loading...

6 Conclusiones y proyectos futuros

Métodos numéricos para leyes de conservación
Métodos numéricos para leyes de conservación