C++ API Documentation

The MOLE C++ API provides low-level access to the mimetic operators and boundary condition functions. This section describes the core classes, functions, and examples for utilizing the API in your C++ applications.

Table of Contents

Divergence Class: Handles the computation of divergence operators.
Gradient Class: Computes the gradient of scalar fields.
Laplacian Class: Supports Laplacian operations on grid-based structures.
Boundary Conditions: Manage Dirichlet, Neumann, and Robin boundary conditions.

C++ API Reference

class Divergence : public sp_mat

#include <divergence.h>

Mimetic Divergence operator.

Public Functions

Divergence(u16 k, u32 m, Real dx)

1-D Mimetic Divergence Constructor

Parameters:

k – Order of accuracy
m – Number of cells
dx – Spacing between cells

Divergence(u16 k, u32 m, u32 n, Real dx, Real dy)

2-D Mimetic Divergence Constructor

Parameters:

k – Order of accuracy
m – Number of cells in x-direction
n – Number of cells in y-direction
dx – Spacing between cells in x-direction
dy – Spacing between cells in y-direction

Divergence(u16 k, u32 m, u32 n, u32 o, Real dx, Real dy, Real dz)

3-D Mimetic Divergence Constructor

Parameters:

k – Order of accuracy
m – Number of cells in x-direction
n – Number of cells in y-direction
o – Number of cells in z-direction
dx – Spacing between cells in x-direction
dy – Spacing between cells in y-direction
dz – Spacing between cells in z-direction

vec getQ(): Returns the weights used in the Mimeitc Divergence Operators.

Note

for informational purposes only, can be used in constructing new operators.

Private Members

vec Q

class Gradient : public sp_mat

#include <gradient.h>

Mimetic Gradient operator.

Public Functions

Gradient(u16 k, u32 m, Real dx)

1-D Mimetic Gradient Constructor

Parameters:

k – Order of accuracy
m – Number of cells
dx – Spacing between cells

Gradient(u16 k, u32 m, u32 n, Real dx, Real dy)

2-D Mimetic Gradient Constructor

Parameters:

k – Order of accuracy
m – Number of cells in x-direction
n – Number of cells in y-direction
dx – Spacing between cells in x-direction
dy – Spacing between cells in y-direction

Gradient(u16 k, u32 m, u32 n, u32 o, Real dx, Real dy, Real dz)

3-D Mimetic Gradient Constructor

Parameters:

k – Order of accuracy
m – Number of cells in x-direction
n – Number of cells in y-direction
o – Number of cells in z-direction
dx – Spacing between cells in x-direction
dy – Spacing between cells in y-direction
dz – Spacing between cells in z-direction

vec getP(): Returns the weights used in the Mimeitc Gradient Operators.

Note

for informational purposes only, can be used in constructing new operators.

Private Members

vec P

class Interpol : public sp_mat

#include <interpol.h>

Mimetic Interpolator operator.

Public Functions

Interpol(u32 m, Real c)

1-D Mimetic Interpolator Constructor

Parameters:

m – Number of cells
c – Weight for ends, can be any value from 0.0<=c<=1.0

Interpol(u32 m, u32 n, Real c1, Real c2)

2-D Mimetic Interpolator Constructor

Parameters:

m – Number of cells in x-direction
n – Number of cells in y-direction
c1 – Weight for ends in x-direction, can be any value from 0.0<=c<=1.0
c2 – Weight for ends in y-direction, can be any value from 0.0<=c<=1.0

Interpol(u32 m, u32 n, u32 o, Real c1, Real c2, Real c3)

3-D Mimetic Interpolator Constructor

Parameters:

m – Number of cells in x-direction
n – Number of cells in y-direction
o – Number of cells in z-direction
c1 – Weight for ends in x-direction, can be any value from 0.0<=c<=1.0
c2 – Weight for ends in y-direction, can be any value from 0.0<=c<=1.0
c3 – Weight for ends in z-direction, can be any value from 0.0<=c<=1.0

Interpol(bool type, u32 m, Real c)

1-D Mimetic Interpolator Constructor

Parameters:

type – Dummy holder to trigger overloaded function
m – Number of cells
c – Weight for ends, can be any value from 0.0<=c<=1.0

Interpol(bool type, u32 m, u32 n, Real c1, Real c2)

2-D Mimetic Interpolator Constructor

Parameters:

type – Dummy holder to trigger overloaded function
m – Number of cells in x-direction
n – Number of cells in y-direction
c1 – Weight for ends in x-direction, can be any value from 0.0<=c<=1.0
c2 – Weight for ends in y-direction, can be any value from 0.0<=c<=1.0

Interpol(bool type, u32 m, u32 n, u32 o, Real c1, Real c2, Real c3)

3-D Mimetic Interpolator Constructor

Parameters:

type – Dummy holder to trigger overloaded function
m – Number of cells in x-direction
n – Number of cells in y-direction
o – Number of cells in z-direction
c1 – Weight for ends in x-direction, can be any value from 0.0<=c<=1.0
c2 – Weight for ends in y-direction, can be any value from 0.0<=c<=1.0
c3 – Weight for ends in z-direction, can be any value from 0.0<=c<=1.0

class Laplacian : public sp_mat

#include <laplacian.h>

Mimetic Laplacian operator.

Public Functions

Laplacian(u16 k, u32 m, Real dx)

1-D Mimetic Laplacian Constructor

Parameters:

k – Order of accuracy
m – Number of cells
dx – Spacing between cells

Laplacian(u16 k, u32 m, u32 n, Real dx, Real dy)

2-D Mimetic Laplacian Constructor

Parameters:

k – Order of accuracy
m – Number of cells in x-direction
n – Number of cells in y-direction
dx – Spacing between cells in x-direction
dy – Spacing between cells in y-direction

Laplacian(u16 k, u32 m, u32 n, u32 o, Real dx, Real dy, Real dz)

3-D Mimetic Laplacian Constructor

Parameters:

k – Order of accuracy
m – Number of cells in x-direction
n – Number of cells in y-direction
o – Number of cells in z-direction
dx – Spacing between cells in x-direction
dy – Spacing between cells in y-direction
dz – Spacing between cells in z-direction

class MixedBC : public sp_mat

#include <mixedbc.h>

Mimetic Mixed Boundary Condition operator.

Public Functions

MixedBC(u16 k, u32 m, Real dx, const std::string &left, const std::vector<Real> &coeffs_left, const std::string &right, const std::vector<Real> &coeffs_right)

1-D Constructor

Parameters:

k – Order of accuracy
m – Number of cells
dx – Spacing between cells
left – Type of boundary condition at the left boundary (‘Dirichlet’, ‘Neumann’, ‘Robin’)
coeffs_left – Coefficients for the left boundary condition
right – Type of boundary condition at the right boundary (‘Dirichlet’, ‘Neumann’, ‘Robin’)
coeffs_right – Coefficients for the right boundary condition

MixedBC(u16 k, u32 m, Real dx, u32 n, Real dy, const std::string &left, const std::vector<Real> &coeffs_left, const std::string &right, const std::vector<Real> &coeffs_right, const std::string &bottom, const std::vector<Real> &coeffs_bottom, const std::string &top, const std::vector<Real> &coeffs_top)

2-D Constructor

Parameters:

k – Order of accuracy
m – Number of cells along x-axis
dx – Spacing between cells along x-axis
n – Number of cells along y-axis
dy – Spacing between cells along y-axis
left – Type of boundary condition at the left boundary (‘Dirichlet’, ‘Neumann’, ‘Robin’)
coeffs_left – Coefficients for the left boundary condition
right – Type of boundary condition at the right boundary (‘Dirichlet’, ‘Neumann’, ‘Robin’)
coeffs_right – Coefficients for the right boundary condition
bottom – Type of boundary condition at the bottom boundary (‘Dirichlet’, ‘Neumann’, ‘Robin’)
coeffs_bottom – Coefficients for the bottom boundary condition
top – Type of boundary condition at the top boundary (‘Dirichlet’, ‘Neumann’, ‘Robin’)
coeffs_top – Coefficients for the top boundary condition

MixedBC(u16 k, u32 m, Real dx, u32 n, Real dy, u32 o, Real dz, const std::string &left, const std::vector<Real> &coeffs_left, const std::string &right, const std::vector<Real> &coeffs_right, const std::string &bottom, const std::vector<Real> &coeffs_bottom, const std::string &top, const std::vector<Real> &coeffs_top, const std::string &front, const std::vector<Real> &coeffs_front, const std::string &back, const std::vector<Real> &coeffs_back)

3-D Constructor

Parameters:

k – Order of accuracy
m – Number of cells along x-axis
dx – Spacing between cells along x-axis
n – Number of cells along y-axis
dy – Spacing between cells along y-axis
o – Number of cells along z-axis
dz – Spacing between cells along z-axis
left – Type of boundary condition at the left boundary (‘Dirichlet’, ‘Neumann’, ‘Robin’)
coeffs_left – Coefficients for the left boundary condition
right – Type of boundary condition at the right boundary (‘Dirichlet’, ‘Neumann’, ‘Robin’)
coeffs_right – Coefficients for the right boundary condition
bottom – Type of boundary condition at the bottom boundary (‘Dirichlet’, ‘Neumann’, ‘Robin’)
coeffs_bottom – Coefficients for the bottom boundary condition
top – Type of boundary condition at the top boundary (‘Dirichlet’, ‘Neumann’, ‘Robin’)
coeffs_top – Coefficients for the top boundary condition
front – Type of boundary condition at the front boundary (‘Dirichlet’, ‘Neumann’, ‘Robin’)
coeffs_front – Coefficients for the front boundary condition
back – Type of boundary condition at the back boundary (‘Dirichlet’, ‘Neumann’, ‘Robin’)
coeffs_back – Coefficients for the back boundary condition

class RobinBC : public sp_mat

#include <robinbc.h>

Mimetic Robin Boundary Condition operator.

Public Functions

RobinBC(u16 k, u32 m, Real dx, Real a, Real b)

1-D Robin boundary constructor

Parameters:

k – mimetic order of accuracy
m – number of cells in x-dimension
dx – cell width in x-direction
a – Coefficient of the Dirichlet function
b – Coefficient of the Neumann function

RobinBC(u16 k, u32 m, Real dx, u32 n, Real dy, Real a, Real b)

2-D Robin boundary constructor

Note

Uses 1-D Robin to build the 2-D operator

Parameters:

k – mimetic order of accuracy
m – number of cells in x-dimension
dx – cell width in x-direction
n – number of cells in y-dimension
dy – cell width in y-direction
a – Coefficient of the Dirichlet function
b – Coefficient of the Neumann function

RobinBC(u16 k, u32 m, Real dx, u32 n, Real dy, u32 o, Real dz, Real a, Real b)

3-D Robin boundary constructor

Note

Uses 1-D Robin to build the 3-D operator

Parameters:

k – mimetic order of accuracy
m – number of cells in x-dimension
dx – cell width in x-direction
n – number of cells in y-dimension
dy – cell width in y-direction
o – number of cells in z-dimension
dz – cell width in z-direction
a – Coefficient of the Dirichlet function
b – Coefficient of the Neumann function

class Utils

#include <utils.h>

Utility Functions.

Public Functions

void meshgrid(const vec &x, const vec &y, mat &X, mat &Y)

An analog to the MATLAB 2D meshgrid operation.

returns 2-D grid coordinates based on the coordinates contained in vectors x and y. X is a matrix where each row is a copy of x, and Y is a matrix where each column is a copy of y. The grid represented by the coordinates X and Y has length(y) rows and length(x) columns. Key here is the rows is the y-coordinate, and the columns are the x-coordinate.

Parameters:

x – a vector of x-indices
y – a vector of y-indices
X – a sparse matrix, will be filled by the function
Y – a sparse matrix, will be filled by the function

void meshgrid(const vec &x, const vec &y, const vec &z, cube &X, cube &Y, cube &Z)

An analog to the MATLAB 3D meshgrid operation.

meshgrid(x,y,z,X,Y,Z) returns 3-D grid coordinates defined by the vectors x, y, and z. The grid represented by X, Y, and Z has size length(y)-by-length(x)-by-length(z).

Parameters:

x – a vector of x-indices
y – a vector of y-indices
z – a vector of z-indices
X – a sparse matrix, will be filled by the function
Y – a sparse matrix, will be filled by the function
Z – a sparse matrix, will be filled by the function

Public Static Functions

static sp_mat spkron(const sp_mat &A, const sp_mat &B)

A wrappper for implementing a sparse Kroenecker product.

Note

This is available in Armadillo >8.0

Parameters:

A – a sparse matrix
B – a sparse matrix

static sp_mat spjoin_rows(const sp_mat &A, const sp_mat &B)

An in place operation for joining two matrices by rows.

Note

This is available in Armadillo >8.0

Parameters:

A – a sparse matrix
B – a sparse matrix

static sp_mat spjoin_cols(const sp_mat &A, const sp_mat &B)

An in place operation for joining two matrices by columns.

Note

This is available in Armadillo >=8.5

Parameters:

A – a sparse matrix
B – a sparse matrix

static vec spsolve_eigen(const sp_mat &A, const vec &b)

A wrappper for implementing a sparse solve using Eigen from SuperLU.

Note

This function requires the EIGEN to be used when Armadillo is built

Parameters:

A – a sparse matrix LHS of Ax=b
b – a vector for the RHS of Ax=b

namespace arma

file README.md

file divergence.cpp: #include “divergence.h”

file divergence.h: #include “utils.h”

#include <cassert>

file gradient.cpp: #include “gradient.h”

file gradient.h: #include “utils.h”

#include <cassert>

file interpol.cpp: #include “interpol.h”

file interpol.h: #include “utils.h”

#include <cassert>

file laplacian.cpp: #include “laplacian.h”

file laplacian.h: #include “divergence.h”

#include “gradient.h”

file mixedbc.cpp: #include “mixedbc.h”

file mixedbc.h: #include “gradient.h”

file mole.h: #include “divergence.h”

#include “gradient.h”

#include “interpol.h”

#include “laplacian.h”

#include “mixedbc.h”

#include “operators.h”

#include “robinbc.h”

#include “utils.h”

file operators.h

#include “interpol.h”

#include “laplacian.h”

#include “mixedbc.h”

#include “robinbc.h”

Functions

inline sp_mat operator*(const Divergence &div, const Gradient &grad)

inline sp_mat operator+(const Laplacian &lap, const RobinBC &bc)

inline sp_mat operator+(const Laplacian &lap, const MixedBC &bc)

inline vec operator*(const Divergence &div, const vec &v)

inline vec operator*(const Gradient &grad, const vec &v)

inline vec operator*(const Laplacian &lap, const vec &v)

inline vec operator*(const Interpol &I, const vec &v)

file robinbc.cpp: #include “robinbc.h”

file robinbc.h: #include “gradient.h”

file utils.cpp: #include “utils.h”

#include <cassert>

file utils.h

#include <armadillo>

Defines

UTILS_H

Typedefs

using Real = double

dir src/cpp

dir src

page MOLE: Mimetic Operators Library Enhanced

1: Description

MOLE is a high-quality (C++ & MATLAB/Octave) library that implements high-order mimetic operators to solve partial differential equations. It provides discrete analogs of the most common vector calculus operators: Gradient, Divergence, Laplacian, Bilaplacian, and Curl. These operators (highly sparse matrices) act on staggered grids (uniform, non-uniform, curvilinear) and satisfy local and global conservation laws.

Mathematics is based on the work of Corbino and Castillo, 2020. However, the user may find helpful previous publications, such as Castillo and Grone, 2003, in which similar operators were derived using a matrix analysis approach.

2: Licensing

MOLE is distributed under a GNU General Public License; please refer to the LICENSE file for more details.

3: Installation

3.1 Packages Required

To install the MOLE library on your system, certain packages must be installed and configured beforehand. The required packages vary by operating system.

For the macOS, Homebrew needs to be installed to download the required packages. Invoke the following command in the terminal app

/bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/HEAD/install.sh)"

Remove Java dependencies

brew uninstall --ignore-dependencies java

Update Homebrew again

brew update

If you encounter errors during Homebrew installation, please run the following commands before the installation:

sudo chown -R $(whoami) /usr/local/Cellar
git -C /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core fetch --unshallow

3.1.1 CMake

Minimum Version Required: 3.10

For Ubuntu systems:

sudo apt install cmake For Mac Systems

brew install cmake For Yum-based systems:

sudo yum install cmake

3.1.2 OpenBLAS

Minimum Version Required: OpenBLAS 0.3.10

For Ubuntu systems:

sudo apt install libopenblas-dev For Mac Systems

brew install openblas For Yum-based systems:

sudo yum install openblas-devel

3.1.3 Eigen3

Minimum Version Required: eigen-3

For Ubuntu systems

sudo apt install libeigen3-dev For Mac Systems

brew install eigen For Yum-based systems:

sudo yum install eigen3-devel

3.1.4 libomp

For Mac Systems

brew install libomp

3.1.5 LAPACK

For Mac Systems

brew install lapack

3.2 MOLE Library Installation

Clone the MOLE repository and build the library

git clone https://github.com/csrc-sdsu/mole.git  
cd mole  
mkdir build && cd build  
cmake ..
make

To install the library in a custom location (Eg. home/mole)

cmake —install . —prefix /path/to/location

To install the library in a previledged location (Eg. /opt/mole)

sudo cmake —install . Or

sudo cmake —install . —prefix /path/to/privileged/location

To run the C++ tests manually,

make run_tests

To run the matlab tests manually,

make run_matlab_tests

Armadillo and SuperLu will be locally installed in the build directory once the cmake .. command is passed. By following the steps outlined above, you will successfully install the necessary packages and the MOLE library on your system. The library will be installed in the location provided. The tests and examples to be executed will also be built locally inside the build directory.

4: Running Examples & Tests

Here are instructions on how to run the provided examples and tests for both the C++ and MATLAB versions of the library to help you quickly get started with MOLE.

tests/cpp: These tests, which are automatically executed upon constructing the library’s C++ version, play a crucial role in verifying the correct installation of MOLE and its dependencies. There are four tests in total.
tests/matlab: We encourage MATLAB users to execute these tests before using MOLE by entering the tests/matlab directory and executing run_tests.m from MATLAB. These tests are analogous to those contained in tests/cpp.
examples/cpp: These will be automatically built after calling make. We encourage C++ users to make this their entry point to familiarize themselves with this library version. The four examples are self-contained and adequately documented, and they solve typical PDEs.
examples/matlab: Most of our examples are provided in the MATLAB scripting language. Over 30 examples range from linear one-dimensional PDEs to highly nonlinear multidimensional PDEs.

5: Documentation

For detailed documentation, including API references, tutorials, and examples, please refer to our Documentation Guide.

NOTE: Performing non-unary operations involving operands constructed over different grids may lead to unexpected results. While MOLE allows such operations without throwing errors, users must exercise caution when manipulating operators across different grids.

6: Community Guidelines

We welcome contributions to MOLE, whether they involve adding new functionalities, providing examples, addressing existing issues, reporting bugs, or requesting new features. Please refer to our Contribution Guidelines for more details.

7: Citations

Please cite our work if you use MOLE in your research or software. Citations are helpful for the continued development and maintenance of the library

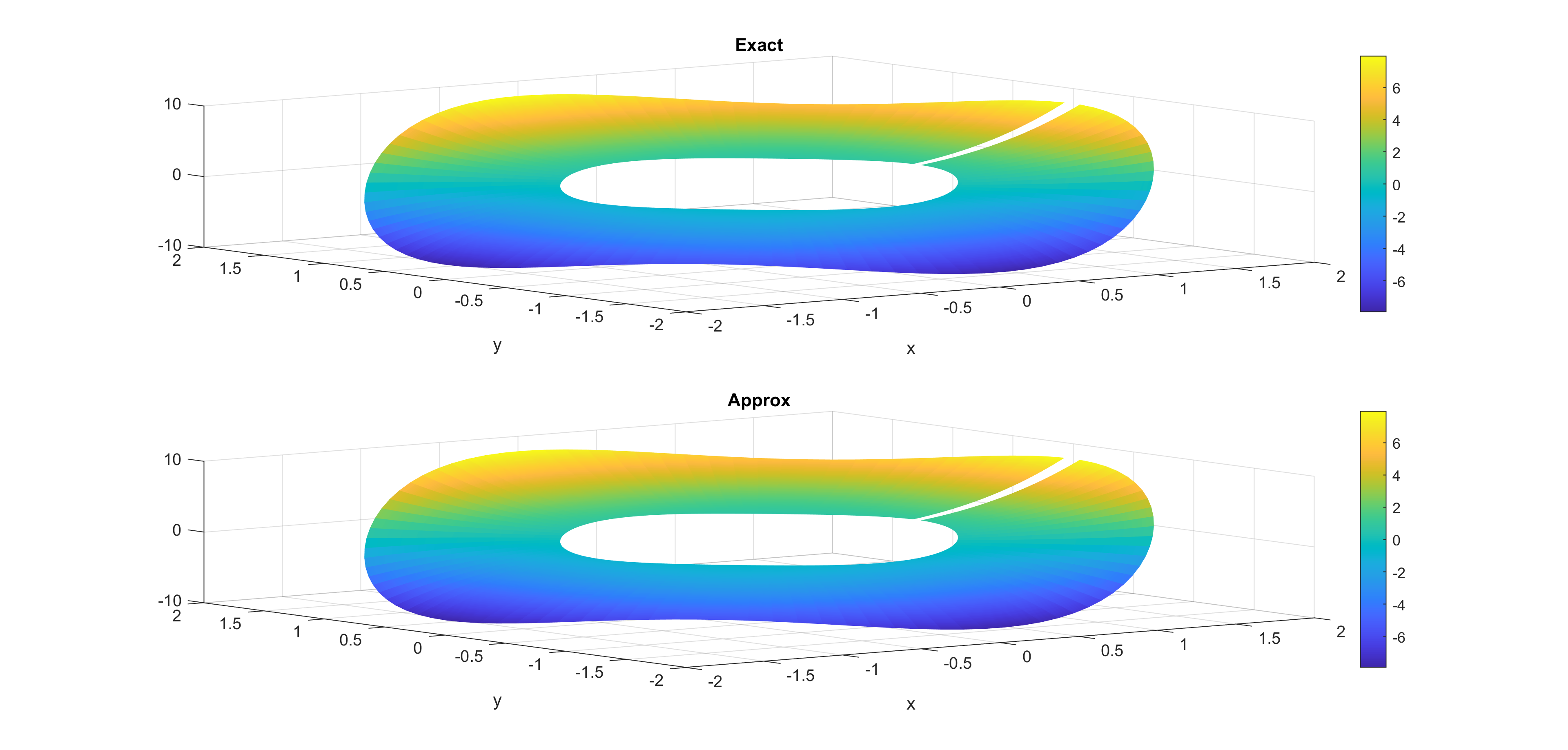
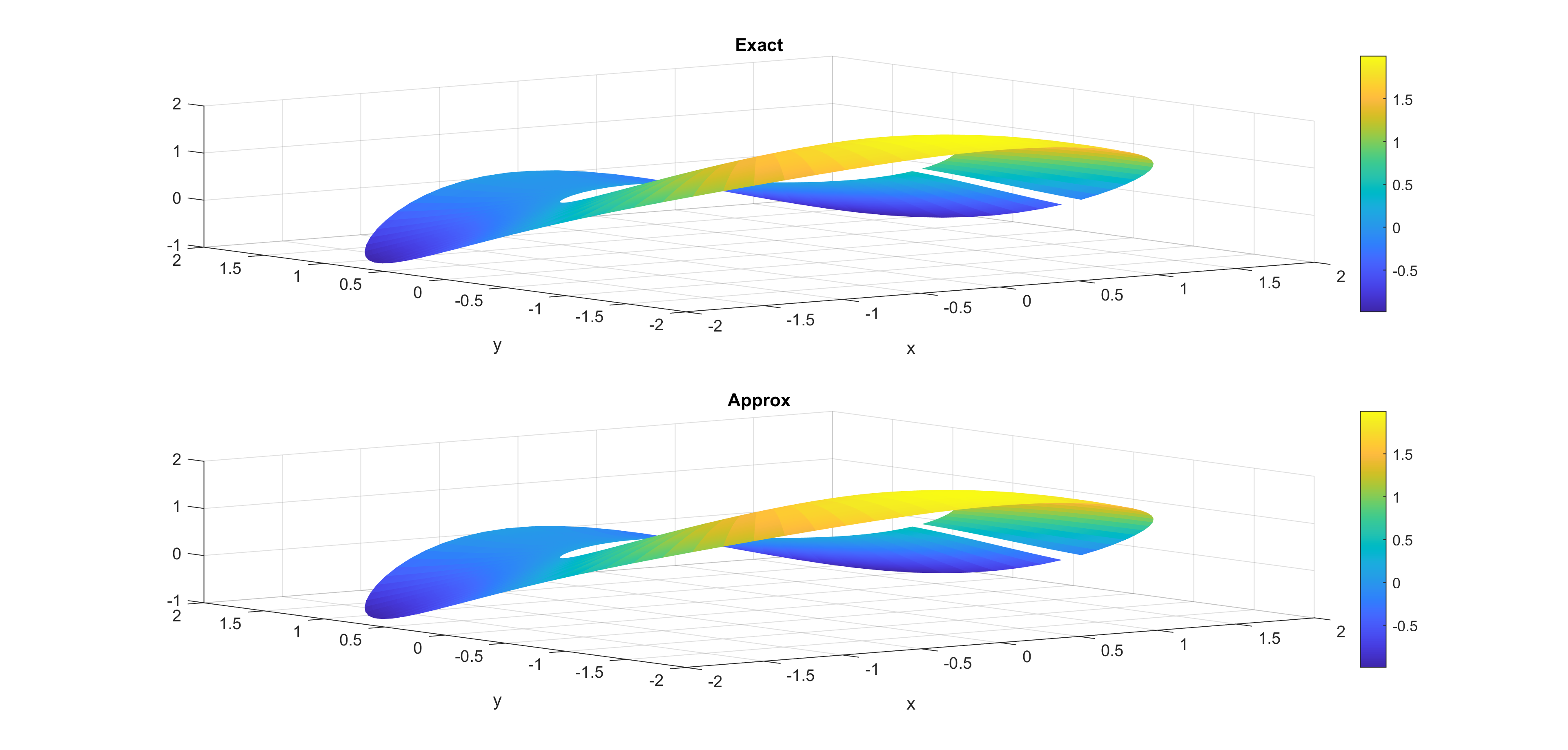
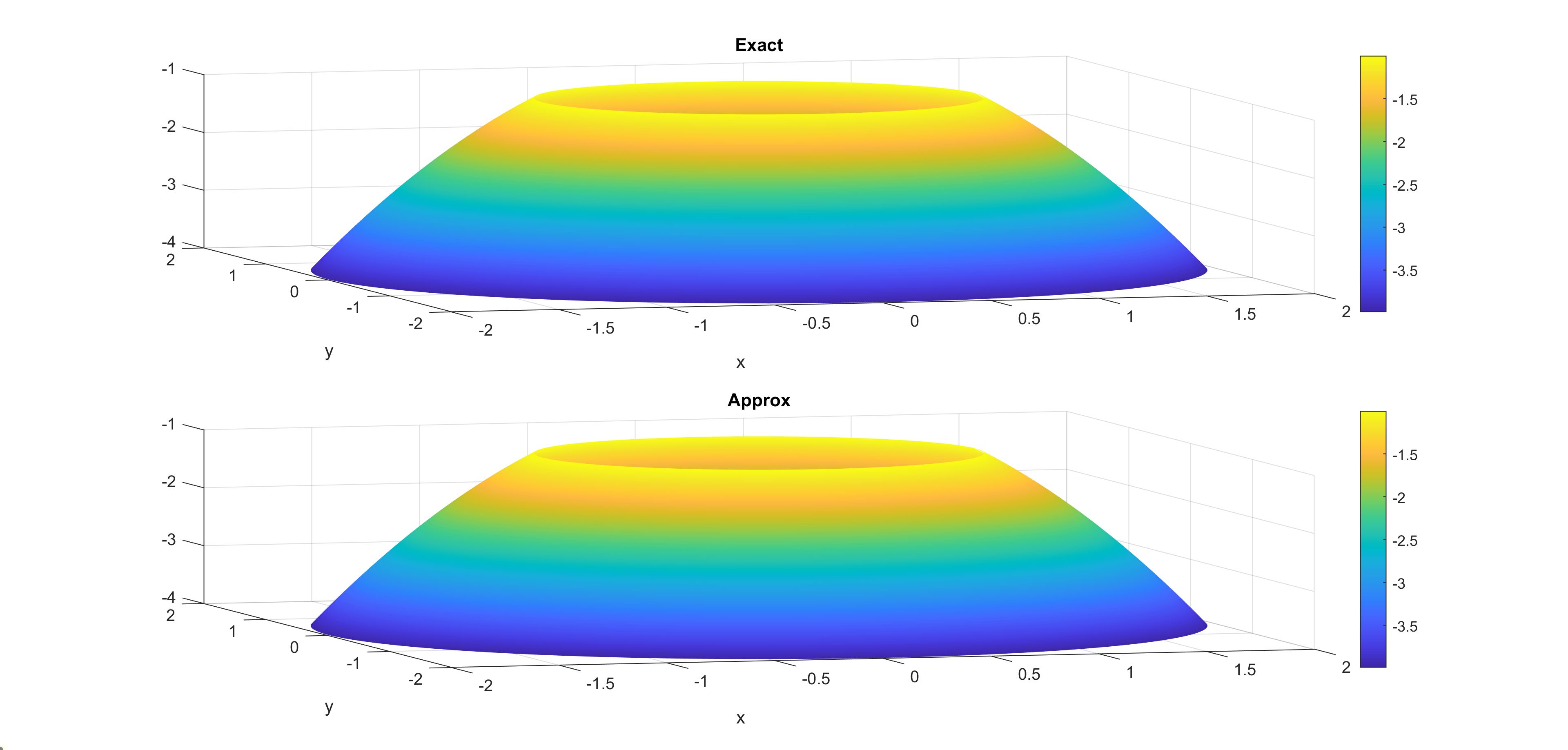
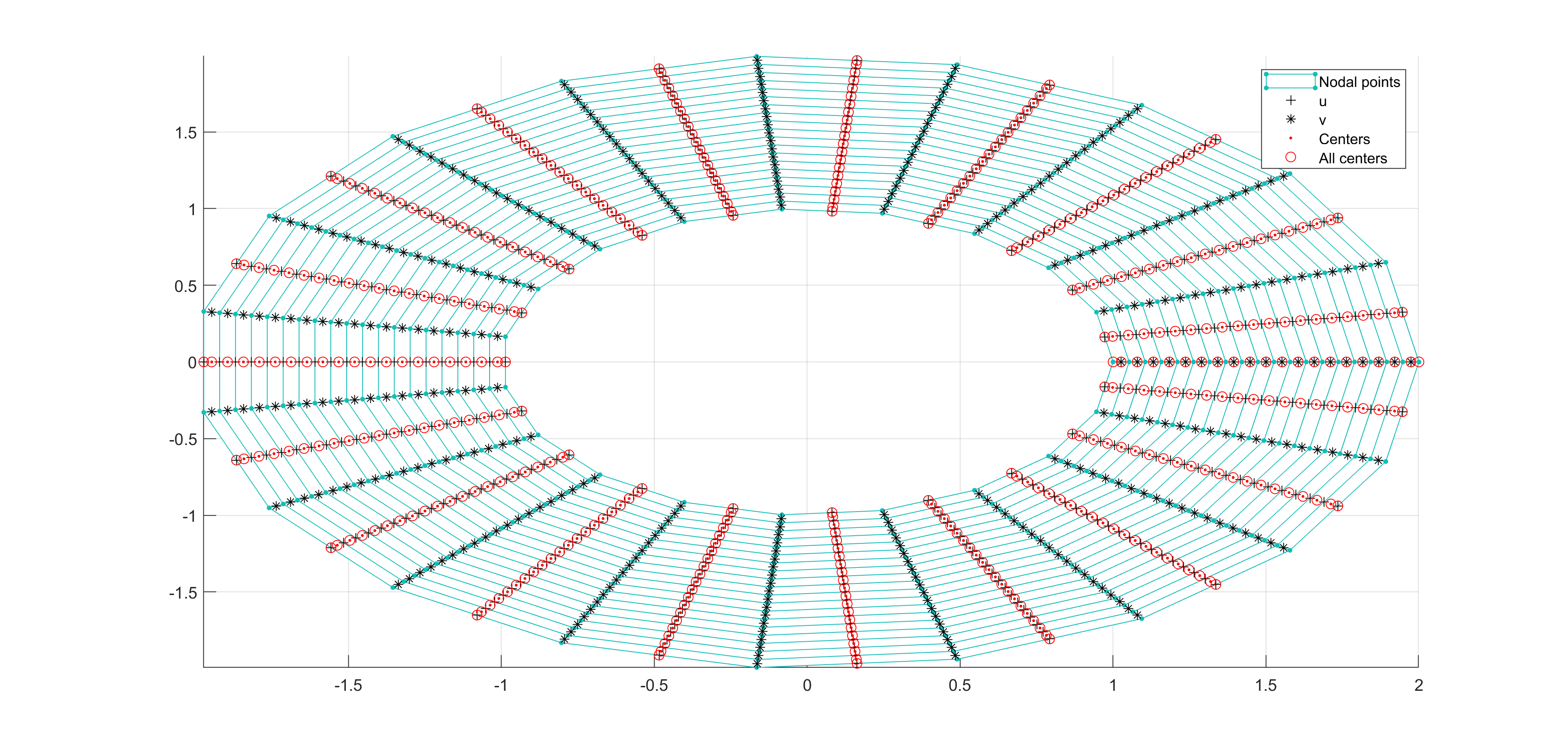
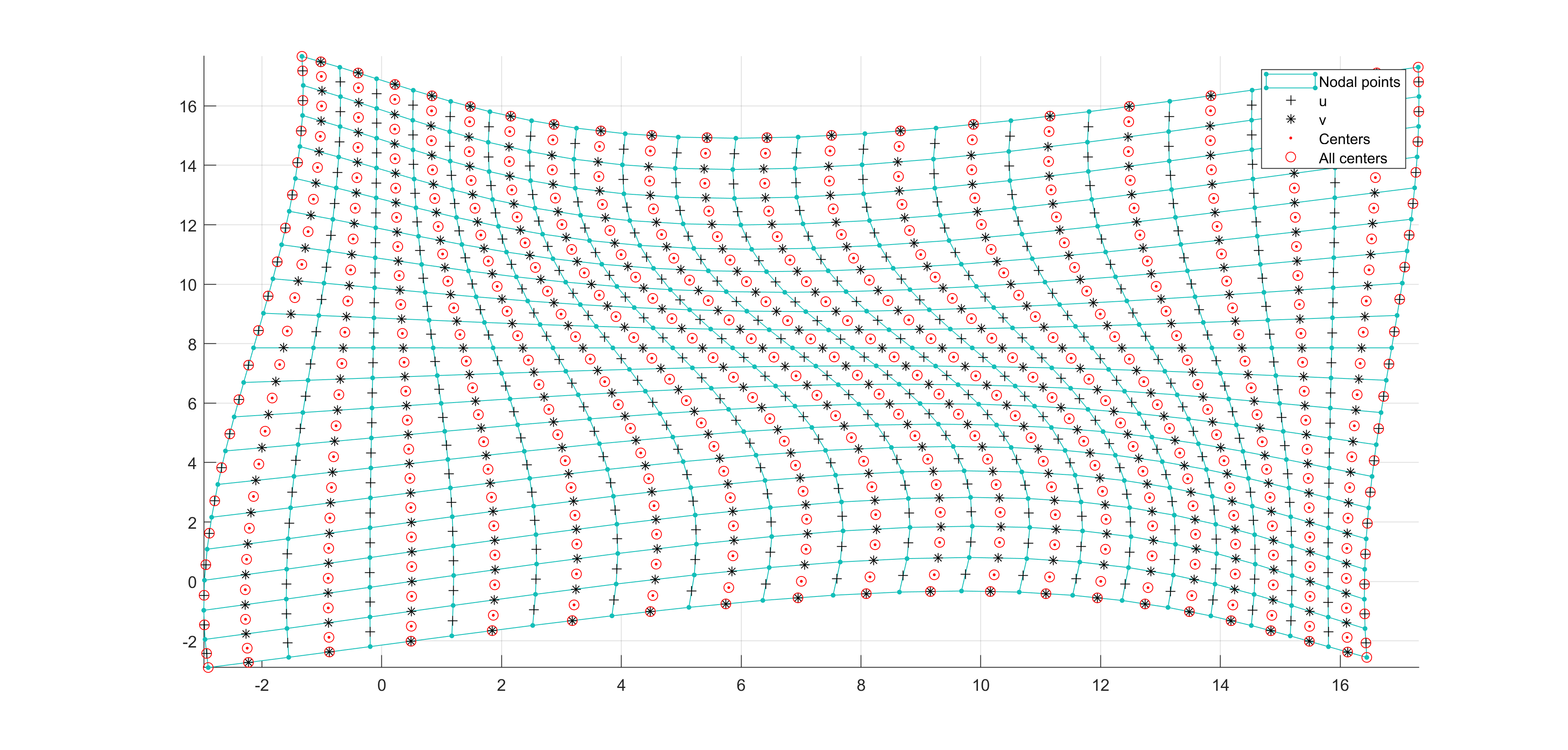
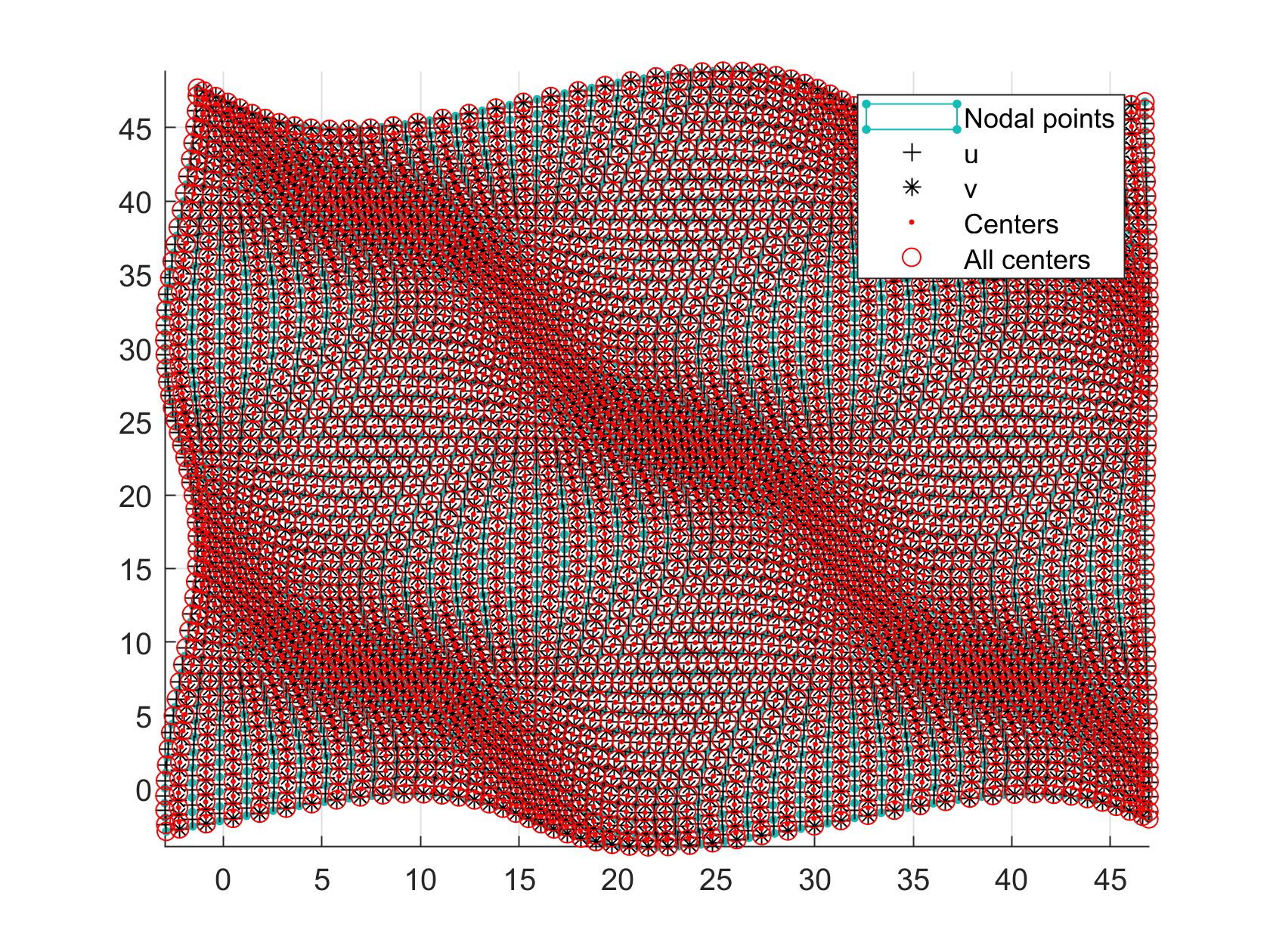
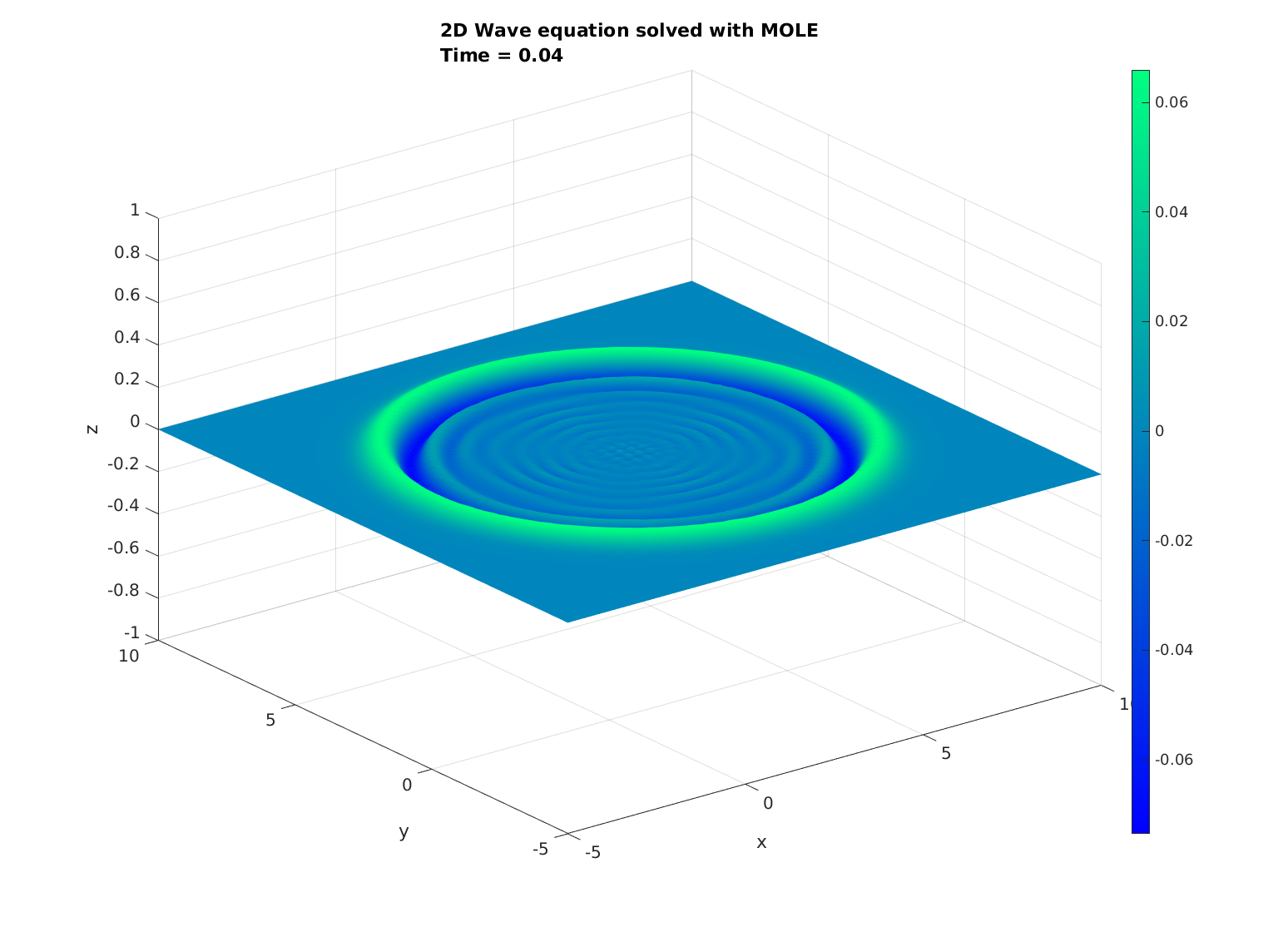
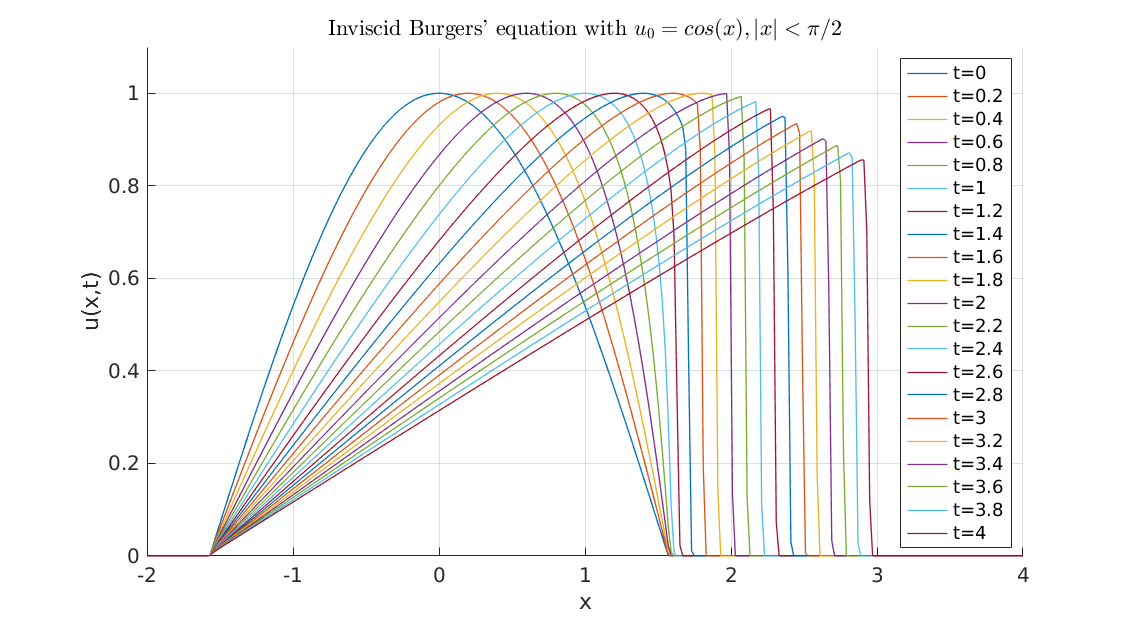
Now, some cool pictures obtained with MOLE:

../_images/4thOrder.png